Question

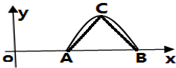已知函数f（x）=Mcos（ωx+ϕ）（M＞0，ω＞0，0＜ϕ＜π）为奇函数，该函数的部分图象如图所示，AC=BC=

2

2

，∠C=90°，则f(

1

2

)=（　　）

• A、-

  1

  2

• B、

  1

  2

• C、-

  2

  2

• D、

  2

  2

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由函数的奇偶性求出φ的值，由点C的坐标为

1

2

求得M，由周期求出ω，可得函数的解析式，从而求得f（

1

2

）的值．

解答： 解：∵函数f（x）=Mcos（ωx+ϕ）（M＞0，ω＞0，0＜ϕ＜π）为奇函数，∴ϕ=

π

2

，∴f（x）=Mcos（ωx+

π

2

）=-Msinωx，
再根据AC=BC=

2

2

，∠C=90°，可得AB=1，点C的坐标为

1

2

，∴M=

1

2

，由T=2AB=2=

2π

ω

，求得ω=π，故f（x）=-

1

2

sinπx，
∴f（

1

2

）=-

1

2

sin

π

2

=-

1

2

，
故选：A．

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由函数的奇偶性求出φ的值，属于基础题．