题目内容
若(
-
)6展开式中的常数项是60,则实数a的值是( )
| x |
| 2 |
| a | ||
|
| A、±1 | ||
B、±
| ||
| C、±2 | ||
D、±2
|
考点:二项式定理
专题:二项式定理
分析:先求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值,再根据展开式中的常数项是60 求得a的值.
解答:
解:由于(
-
)6展开式中的通项公式为 Tr+1=
•(-a)r•(
)6-r•x6-
,令6-
=0,求得=4,
可得它的展开式的常数项是
•a4•
=
a4,再根据展开式中的常数项是60,
可得
a4=60,∴a4=16,求得a=±2,
故选:C.
| x |
| 2 |
| a | ||
|
| C | r 6 |
| 1 |
| 2 |
| 3r |
| 2 |
| 3r |
| 2 |
可得它的展开式的常数项是
| C | 4 6 |
| 1 |
| 4 |
| 15 |
| 4 |
可得
| 15 |
| 4 |
故选:C.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
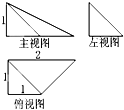
 一个几何体的三视图如图所示,其中正视图和侧视图均是边长为2的等边三角形,则该几何体的表面积是( )
一个几何体的三视图如图所示,其中正视图和侧视图均是边长为2的等边三角形,则该几何体的表面积是( )A、
| ||||
B、4+4
| ||||
| C、12 | ||||
D、
|
 今年3月1日,重庆某中学50位学生参加了“北约联盟”的自主招生考试.这50位同学的数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[60,70),[70,80),[80,90),[90,100),[100,110),[110,120].
今年3月1日,重庆某中学50位学生参加了“北约联盟”的自主招生考试.这50位同学的数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[60,70),[70,80),[80,90),[90,100),[100,110),[110,120].