题目内容
已知△ABC在中,角A,B,C所对的边分别为a,b,c,且acosC+
c=b,则角A( )
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:正弦定理
专题:解三角形
分析:通过已知表达式,利用正弦定理,以及三角形的内角和,转化sinB=sin(A+C),通过两角和的正弦函数,化简可求A的余弦值,即可求角A.
解答:
解:△ABC在中,由acosC+
c=b利用正弦定理可得 sinAcosC+
sinC=sinB,
而sinB=sin(A+C)=sinAcosC+cosAsinC.
可得
sinC=cosAsinC,sinC≠0,
所以
=cosA,A∈(0,π),所以A=
,
故选:B.
| ||
| 2 |
| ||
| 2 |
而sinB=sin(A+C)=sinAcosC+cosAsinC.
可得
| ||
| 2 |
所以
| ||
| 2 |
| π |
| 6 |
故选:B.
点评:本题考查正弦定理与两角和的正弦公式、诱导公式,三角形的内角和以及正弦定理的应用,考查计算能力,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=2sin(ωx+ϕ) (其中ω>0,|ϕ|<
)的图象的相邻两条对称轴间的距离是
,且f(0)=
,则ω和ϕ的值分别是( )
| π |
| 2 |
| π |
| 2 |
| 3 |
A、2,
| ||
B、2,
| ||
C、4,
| ||
D、4,
|
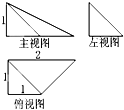
 一个几何体的三视图如图所示,其中正视图和侧视图均是边长为2的等边三角形,则该几何体的表面积是( )
一个几何体的三视图如图所示,其中正视图和侧视图均是边长为2的等边三角形,则该几何体的表面积是( )A、
| ||||
B、4+4
| ||||
| C、12 | ||||
D、
|
若复数z满足:z+1=
(1+i),其中
是复数z的共轭复数,则z•
等于( )
. |
| z |
. |
| z |
. |
| z |
| A、3 | B、5 | C、8 | D、10 |