题目内容
15.某几何体的正视图和侧视图如图(1)所示,它的俯视图的直观图是A'B'C',如图(2)所示,其中O'A'=O'B'=2,$O'C'=\sqrt{3}$,则该几何体的表面积为( )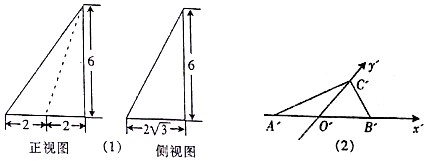
| A. | $36+12\sqrt{3}$ | B. | $24+8\sqrt{3}$ | C. | $24+12\sqrt{3}$ | D. | $36+8\sqrt{3}$ |
分析 由俯视图的直观图可得原图形:为边长为4的等边三角形.可得原几何体为四棱锥P-ABC.其中PC⊥底面ABC.
解答 解:由俯视图的直观图可得原图形:为边长为4的等边三角形.
可得原几何体为四棱锥P-ABC.其中PC⊥底面ABC.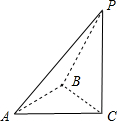
∴该几何体的表面积S=$\frac{\sqrt{3}}{4}×{4}^{2}$+$2×\frac{1}{2}×4×6$+$\frac{1}{2}×4×\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$
=24$+12\sqrt{3}$.
故选:C.
点评 本题考查了四棱锥的三视图、三角形面积计算公式、直观图,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10. 一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
 一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
20.执行如图所示的程序框图,输出n的值为( )


| A. | 19 | B. | 20 | C. | 21 | D. | 22 |

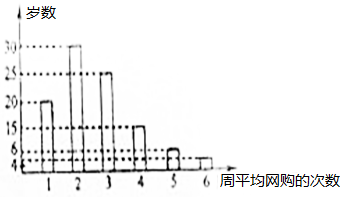 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.