题目内容
5.已知f(x)=$\frac{x+a}{x-a}$ex.(Ⅰ)a=1时,求f(x)在点(0,f(0))处的切线方程;
(Ⅱ)a=0且x>0时,$\frac{f(x)}{lnf(x)}$+m>0恒成立,求m的取值范围;
(Ⅲ)若f(x)在(-1,1)上单调递减,求a的范围.
分析 (Ⅰ)求出函数的导数,计算f(0),f′(0),求出切线方程即可;
(Ⅱ)原式即$\frac{{e}^{x}}{x}$+m>0,令g(x)=$\frac{{e}^{x}}{x}$,求出函数的导数,得到g(x)的最小值,求出m的范围即可;
(Ⅲ)求出函数的导数,问题转化为x2-a2-2a≤0且a≠x,根据二次函数的性质得到关于a的不等式组,解出即可.
解答 解:(Ⅰ)当a=1时,f(x)=$\frac{x+1}{x-1}$ex,f′(x)=ex$\frac{{x}^{2}-3}{{(x-1)}^{2}}$,
∴f(0)=-1,f′(0)=-3,
∴f(x)的切线方程是y+1=-3(x-0),
即3x+y+1=0;
(Ⅱ)当a=0时,f(x)=ex,
∴lnf(x)=x,原式即$\frac{{e}^{x}}{x}$+m>0,
令g(x)=$\frac{{e}^{x}}{x}$,则g′(x)=$\frac{x-1}{{x}^{2}}$ex,
∵x>0,∴0<x<1时,g′(x)<0,g(x)递减,
x>1时,g′(x)>0,g(x)递增,
故g(x)最小值=g(1)=e,
∴m>-e;
(Ⅲ)∵f′(x)=$\frac{{x}^{2}{-a}^{2}-2a}{{(x-a)}^{2}}$ex,x≠a且f(x)在(-1,1)递减,
∴$\frac{{x}^{2}{-a}^{2}-2a}{{(x-a)}^{2}}$ex≤0在(-1,1)恒成立,
故只需x2-a2-2a≤0且a≠x,
故$\left\{\begin{array}{l}{1{-a}^{2}-2a≤0}\\{a≤-1}\end{array}\right.$或$\left\{\begin{array}{l}{1{-a}^{2}-2a≤0}\\{a≥1}\end{array}\right.$,
解得:a≥1或a≤-1-$\sqrt{2}$.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案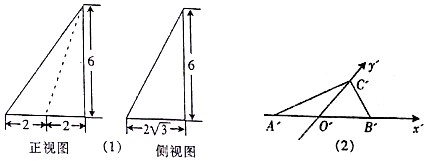
| A. | $36+12\sqrt{3}$ | B. | $24+8\sqrt{3}$ | C. | $24+12\sqrt{3}$ | D. | $36+8\sqrt{3}$ |
| A. | [0,3) | B. | (-3,4] | C. | [3,4] | D. | (-∞,-3)∪[0,+∞) |
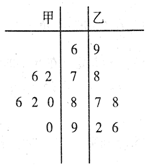 甲、乙两名学生的六次数学测试成绩(百分制)如图所示.
甲、乙两名学生的六次数学测试成绩(百分制)如图所示. 中,茎2的叶子数为3.
中,茎2的叶子数为3.