题目内容
7.已知y=f(x)是二次函数,方程f(0)=1,且f′(x)=2x+2(1)求f(x)的解析式.
(2)求函数y=f(x)与y=-x2-4x+1所围成的图形的面积.
分析 (1)利用二次函数以及导数的关系式得到解析式的系数;求导解析式;
(2)利用定积分表示图象面积,然后计算定积分.
解答 解:(1)∵y=f(x)是二次函数,且f'(x)=2x+2.∴可设f(x)=x2+2x+c.
又∵方程f(0)=1得到c=1,
∴f(x)=x2+2x+1;
(2)∵函数f(x)=x2+2x+1与函数y=-x2-4x+1的图象交于点(0,1),(-3,4),
∴两函数图象所围成的图形的面积为${∫}_{-3}^{0}(-{x}^{2}-4x+1-{x}^{2}-2x-1)dx$=${∫}_{-3}^{0}(-2{x}^{2}-6x)dx$=($-\frac{2}{3}{x}^{3}-3{x}^{2}$)|${\;}_{-3}^{0}$=9.
点评 本题考查了二次函数解析式的求法以及定积分的运用;利用定积分的几何意义表示图象的面积是关键.

练习册系列答案
相关题目
17.为提高市场销售业绩,某公司设计两套产品促销方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),并在某地区部分营销网点进行试点(每个试点网点只采用一种促销方案),运作一年后,对比该地区上一年度的销售情况,分别统计相应营销网点个数,制作相应的列联表如表所示.
(Ⅰ)请根据列联表提供的信息,为该公司今年选择一套较为有利的促销方案(不必说明理由);
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价xi(单位:元/件,整数)和销量yi(单位:件)(i=1,2,…8)如表所示:
(ⅰ)请根据下列数据计算相应的相关指数R2,并根据计算结果,选择合适的回归模型进行拟合;
(ⅱ)根据所选回归模型,分析售价x定为多少时?利润z可以达到最大.
参考公式:相关指数M.
| 无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
| 本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
| 本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
| 100 | 80 | 60 |
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价xi(单位:元/件,整数)和销量yi(单位:件)(i=1,2,…8)如表所示:
| 售价x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 销量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
(ⅱ)根据所选回归模型,分析售价x定为多少时?利润z可以达到最大.
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| $\sum_{i=1}^8{({y_i}}-{\hat y_i}{)^2}$ | 49428.74 | 11512.43 | 175.26 |
| $\sum_{i=1}^8{({y_i}}-\overline y{)^2}$ | 124650 | ||
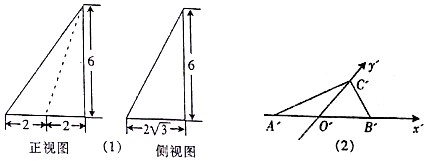
15.某几何体的正视图和侧视图如图(1)所示,它的俯视图的直观图是A'B'C',如图(2)所示,其中O'A'=O'B'=2,$O'C'=\sqrt{3}$,则该几何体的表面积为( )

| A. | $36+12\sqrt{3}$ | B. | $24+8\sqrt{3}$ | C. | $24+12\sqrt{3}$ | D. | $36+8\sqrt{3}$ |
2.定义在R上的函数f(x)的导函数为f′(x),f(0)=0.若对任意x∈R,都有f(x)>f′(x)+1,则使得f(x)+ex<1成立的x的取值范围为( )
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,+∞) | D. | (0,+∞) |
12.记复数z的共轭复数为$\overline z$,若$\overline z•({1-i})=2i$(i为虚数单位),则复数z在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |