题目内容
3.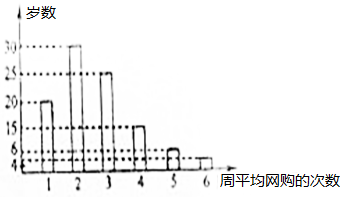 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数直方图.这10名市民中,年龄不超过40岁的有65人.将所抽样中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.(1)根据已知条件完成下面的2×2列联表,能否在犯错的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关?
(2)现将所抽取样本中周平均网购次数不小于5次的市民称为超级网购迷,且已知超级网购迷中有2名年龄超过40岁,若从超级网购迷中任意挑选2名,求至少有1名市民年龄超过40岁的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;
| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
分析 (1)根据已知条件完成列联表,计算观测值,对照临界值得出结论;
(2)利用列举法求出基本事件数,计算对应的概率值.
解答 解:(1)根据已知条件完成2×2列联表,如下;
| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | 20 | 45 | 65 |
| 年龄超过40岁 | 5 | 30 | 35 |
| 合计 | 25 | 75 | 100 |
因为3.297>2.706,
所以据此列联表判断,在犯错误的概率不超过0.10的前提下,认为网购迷与年龄不超过40岁有关;
(2)由频率分布直方图知,超级网购迷共有7人,记其中年龄超过40岁的2名市民为A、B,
其余5名市民记为c、d、e、f、g,现从7人中任取2人,基本事件是
AB、Ac、Ad、Ae、Af、Ag、Bc、Bd、Be、Bf、Bg、
cd、ce、cf、cg、de、df、dg、ef、eg、fg共有21种,
其中至少有1名市民年龄超过40岁的基本事件是
AB、Ac、Ad、Ae、Af、Ag、Bc、Bd、Be、Bf、Bg共11种,
故所求的概率为P=$\frac{11}{21}$.
点评 本题考查了独立性检验和列举法求古典概型的概率问题,是基础题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
13.执行如图所示的程序框图,若输出的结果是8,则判断框内m的取值范围是( )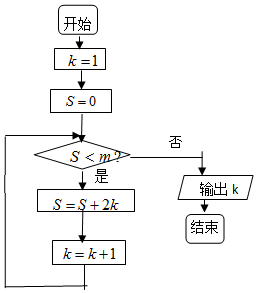

| A. | (42,56] | B. | (20,30] | C. | (30,42] | D. | (20,42) |
14.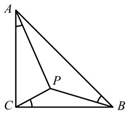 如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
 如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
15.某几何体的正视图和侧视图如图(1)所示,它的俯视图的直观图是A'B'C',如图(2)所示,其中O'A'=O'B'=2,$O'C'=\sqrt{3}$,则该几何体的表面积为( )
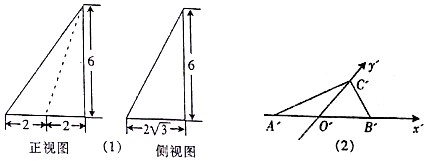

| A. | $36+12\sqrt{3}$ | B. | $24+8\sqrt{3}$ | C. | $24+12\sqrt{3}$ | D. | $36+8\sqrt{3}$ |
12.记复数z的共轭复数为$\overline z$,若$\overline z•({1-i})=2i$(i为虚数单位),则复数z在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知集合A={x∈R|0≤x≤4},B={x∈R|x2≥9},则A∪(∁RB)等于( )
| A. | [0,3) | B. | (-3,4] | C. | [3,4] | D. | (-∞,-3)∪[0,+∞) |