题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{k{x}^{2}+2x-1,x∈(0,1]}\\{kx+1,x∈(1,+∞)}\end{array}\right.$有两个不相等的零点x1,x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的最大值为$\frac{9}{4}$.分析 对k讨论,当k=0,k>0,函数f(x)仅有一个零点;当k<0时,分别求出两个零点,运用换元法,结合二次函数的最值求法,即可得到所求最大值.
解答 解:由函数f(x)=$\left\{\begin{array}{l}{k{x}^{2}+2x-1,x∈(0,1]}\\{kx+1,x∈(1,+∞)}\end{array}\right.$,
当k=0时,f(x)=0,仅有一根x=$\frac{1}{2}$,不符题意;
当k>0时,x>1时,f(x)无零点;
则0<x≤1时,f(x)=0的两根为x=$\frac{-2±\sqrt{4+4k}}{2k}$=$\frac{-1±\sqrt{1+k}}{k}$,
必有一个负的,也不符合题意;
故k<0,由x>1可得kx+1=0,即x1=-$\frac{1}{k}$,-1<k<0;
由0<x≤1时,f(x)=0即为k=$\frac{1-2x}{{x}^{2}}$=($\frac{1}{x}$-1)2-1,$\frac{1}{x}$≥1,
可得x2=$\frac{1}{1+\sqrt{1+k}}$,
则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-k+1+$\sqrt{1+k}$,-1<k<0,
令t=$\sqrt{1+k}$,0<t<1,可得-k+1+$\sqrt{1+k}$=t-(t2-1)+1=-(t-$\frac{1}{2}$)2+$\frac{9}{4}$,
当t=$\frac{1}{2}$即k=-$\frac{3}{4}$时,取得最大值$\frac{9}{4}$,
故答案为:$\frac{9}{4}$.
点评 本题考查函数方程的转化思想的运用,考查函数的零点的求法,注意运用分类讨论和换元法,考查化简整理的运算能力,属于中档题.

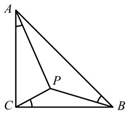 如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
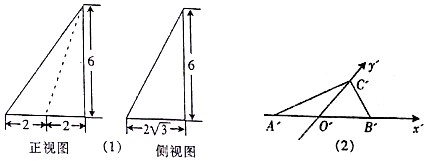
| A. | $36+12\sqrt{3}$ | B. | $24+8\sqrt{3}$ | C. | $24+12\sqrt{3}$ | D. | $36+8\sqrt{3}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 48 | B. | 36 | C. | 24 | D. | 18 |
| A. | [0,3) | B. | (-3,4] | C. | [3,4] | D. | (-∞,-3)∪[0,+∞) |