题目内容
10. 一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )
一个三棱柱被一个平面截去一部分后,剩余部分的三视图如图所示,则该几何体的体积为( )| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
分析 由三视图可知:该几何体由三棱柱ABC-A1B1C1,去掉一个三棱锥A1-ABC后剩下的几何体,AB⊥AC.
解答 解:由三视图可知:该几何体由三棱柱ABC-A1B1C1,
去掉一个三棱锥A1-ABC后剩下的几何体,AB⊥AC.
其体积V=$\frac{1}{2}×3×4×5$-$\frac{1}{3}×\frac{1}{2}×3×4×5$=20.
故选:B.
点评 本题考查了三棱锥与三棱柱的三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
1.P(x,y)是曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}$(0≤θ<π,θ是参数)上的动点,则$\frac{y}{x}$的取值范围是( )
| A. | [-$\frac{\sqrt{3}}{3}$,0] | B. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | C. | [0,$\frac{\sqrt{3}}{3}$] | D. | (-∞,$\frac{\sqrt{3}}{3}$] |
5.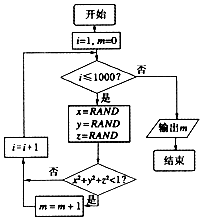 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )| A. | 3.126 | B. | 3.132 | C. | 3.151 | D. | 3.162 |
15.某几何体的正视图和侧视图如图(1)所示,它的俯视图的直观图是A'B'C',如图(2)所示,其中O'A'=O'B'=2,$O'C'=\sqrt{3}$,则该几何体的表面积为( )
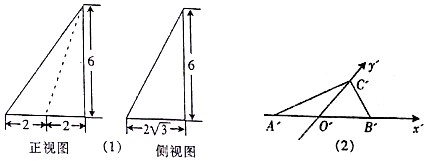

| A. | $36+12\sqrt{3}$ | B. | $24+8\sqrt{3}$ | C. | $24+12\sqrt{3}$ | D. | $36+8\sqrt{3}$ |
2.定义在R上的函数f(x)的导函数为f′(x),f(0)=0.若对任意x∈R,都有f(x)>f′(x)+1,则使得f(x)+ex<1成立的x的取值范围为( )
| A. | (-∞,0) | B. | (-∞,1) | C. | (-1,+∞) | D. | (0,+∞) |
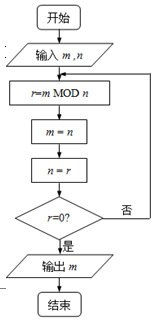 右边程序框图的算法思路源于数学名著《几何原本》中的“辗转
右边程序框图的算法思路源于数学名著《几何原本》中的“辗转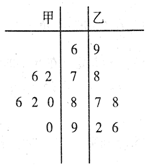 甲、乙两名学生的六次数学测试成绩(百分制)如图所示.
甲、乙两名学生的六次数学测试成绩(百分制)如图所示.