题目内容
设函数f(x)=
,若函数y=f(x)-k存在两个零点,则实数k的取值范围是 .
|
考点:函数零点的判定定理
专题:作图题
分析:问题等价于函数y=f(x)与y=k的图象有两个公共点,作出函数的图象可得结论.
解答:
 解:∵函数y=f(x)-k存在两个零点,
解:∵函数y=f(x)-k存在两个零点,
∴函数y=f(x)与y=k的图象有两个公共点,
在同一个坐标系中作出它们的图象,
由图象可知:实数k的取值范围是(0,1],
故答案为:(0,1]
 解:∵函数y=f(x)-k存在两个零点,
解:∵函数y=f(x)-k存在两个零点,∴函数y=f(x)与y=k的图象有两个公共点,
在同一个坐标系中作出它们的图象,
由图象可知:实数k的取值范围是(0,1],
故答案为:(0,1]
点评:本题考查函数的零点,数形结合是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知
和
是平面内两个单位向量,它们的夹角为60°,则2
-
与
的夹角是( )
| AB |
| AC |
| AB |
| AC |
| CA |
| A、30° | B、60° |
| C、90° | D、120° |
设椭圆Γ:
+
=1(a>b>0)的焦点为F1,F2,若椭圆Γ上存在点P,使△PF1F2是以F1P为底边的等腰三角形,则椭圆Γ的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
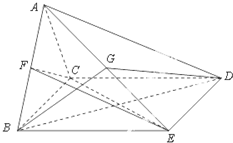 如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
 已知椭圆C:
已知椭圆C: