题目内容

已知
AB
和
AC
是平面内两个单位向量，它们的夹角为60°，则2
AB
-
AC
与
CA
的夹角是（　　）
A、30°B、60°
C、90°D、120°
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的数量积、向量垂直与数量积的关系即可得出．
解答： 解：∵
AB
和
AC
是平面内两个单位向量，它们的夹角为60°，
∴
AB
•
AC
=|
AB
| |
AC
|cos60°=
1
2
．
∴（2
AB
-
AC
）•
CA
=2
AB
•
CA
-
AC
•
CA
=2×(-
1
2
)+1=0，
∴2
AB
-
AC
与
CA
的夹角是90°．
故选：C．
点评：本题考查了向量的数量积、向量垂直与数量积的关系，属于基础题．
练习册系列答案
相关题目
已知椭圆M：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率e=
1
2
，左准线方程为x=-4．
（1）求椭圆M的标准方程；
（2）已知过椭圆
x2
a2
+
y2
b2
=1上一点（x0，y0）作椭圆的切线，切线方程为
x0x
a2
+
y0y
b2
=1．现过椭圆M的右焦点作斜率不为0的直线l于椭圆交于A，B两点，过A，B分别作椭圆的切线l1，l2．
①证明：l1，l2的交点P在一条定直线上；
②求△ABP面积的最小值．
对于不等式组
2x-3y+2≥0
3x-y-4≤0
x+2y+1≥0
的解（x，y），当且仅当
x=2
y=2
时，z=x+ay取得最大值，则实数a的取值范围是
 
．
复数z=
i
 1- i 
（其中i为虚数单位）的模为
 
．
设函数f（x）=
x
，x＞0
4x，x≤0
，若函数y=f（x）-k存在两个零点，则实数k的取值范围是
 
．
下列函数中周期为π且图象关于直线x=
π
3
对称的函数是（　　）
A、y=2sin（
x
2
+
π
3
）
B、y=2sin（2x-
π
6
）
C、y=2sin（2x+
π
6
）
D、y=2sin（
x
2
-
π
3
）
执行如图所示的程序框图，则输出S的值是（　　）
A、10B、17C、26D、28
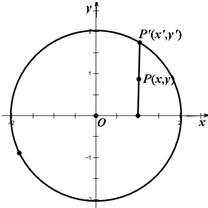如图，将圆p：x2+y2=4上任意一点P′的纵坐标变为原来的一半 （横坐标不变），得到点P，并设点P的轨迹为曲线C．
（1）求C的方程；
（2）设o为坐标原点，过点Q（
3
，0）的直线l与曲线C交于两点A，B，线段AB的中点为N，且
OE
=2
ON
，点E在曲线C上，求直线l：
x
a
+
y
b
=1的方程．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右两焦点分别为F1，F2，p是椭圆上一点，且在x轴上方，PF2⊥F1F2，PF2=λPF1，λ∈[
1
3
，
1
2
]．
（1）求椭圆的离心率e的取值范围；
（2）当e取最大值时，过F1，F2，P的圆Q的截y轴的线段长为6，求椭圆的方程；
（3）在（2）的条件下，过椭圆右准线l上任一点A引圆Q的两条切线，切点分别为M，N．试探究直线MN是否过定点？若过定点，请求出该定点；否则，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网