题目内容
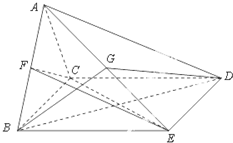 如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.(1)若点G是AE的中点,求证:AC∥平面BDG
(2)若F是线段AB的中点,求三棱锥B-EFC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)设CE∩BD=O,连接OG,只需证明OG∥AC,即可证明AC∥平面BDG.
(2)由三棱锥B-EFC的体积等于三棱锥E-BCF的体积,求出底面△BCF的面积,高BE=CD,即得所求.
(2)由三棱锥B-EFC的体积等于三棱锥E-BCF的体积,求出底面△BCF的面积,高BE=CD,即得所求.
解答:
解:如图,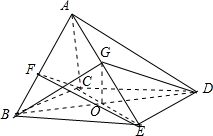
(1)证明:设CE∩BD=O,连接OG,
由三角形的中位线定理可得:OG∥AC,
∵AC?平面BDG,OG?平面BDG,∴AC∥平面BDG.
(2)∵平面ABC⊥平面BCDE,DC⊥BC,
∴DC⊥平面ABC,∴DC⊥AC,∴DC=
=2
;
又∵F是AB的中点,△ABC是正三角形,
∴CF⊥AB,
∴S△BCF=
BF•CF=
,
又平面ABC⊥平面BCDE,EB⊥BC,
∴EB⊥平面BCF,
∴VB-EFC=VE-BCF=
S△BCF•EB=1.

(1)证明:设CE∩BD=O,连接OG,
由三角形的中位线定理可得:OG∥AC,
∵AC?平面BDG,OG?平面BDG,∴AC∥平面BDG.
(2)∵平面ABC⊥平面BCDE,DC⊥BC,
∴DC⊥平面ABC,∴DC⊥AC,∴DC=
| AD2-AC2 |
| 3 |
又∵F是AB的中点,△ABC是正三角形,
∴CF⊥AB,
∴S△BCF=
| 1 |
| 2 |
| ||
| 2 |
又平面ABC⊥平面BCDE,EB⊥BC,
∴EB⊥平面BCF,
∴VB-EFC=VE-BCF=
| 1 |
| 3 |
点评:本题考查了空间中的直线与平面平行的判定问题以及求三棱锥的体积问题,也考查了一定的空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
有一个几何体的三视图如图所示,这个几何体是一个( )


| A、棱台 | B、棱锥 | C、棱柱 | D、圆柱 |
若0<x<y<1,则( )
| A、logx3<logy3 | ||||
| B、3y<3x | ||||
| C、log4x<log4y | ||||
D、(
|
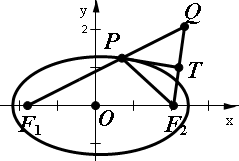 已知椭圆
已知椭圆