题目内容
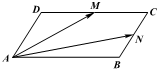
在平行四边形ABCD中，M，N分别是CD，BC的中点，
=(1，2) ，
=（3，1），则
•
= ．
| AM |
| AN |
| AB |
| AM |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的三角形法则，求出向量AB，再由向量的数量积的坐标公式即可得到．
解答：
解：由于
=
+
=
+
，
=
+
，
则有
=
-
=
（3，1）-
（1，2）=（
，0），
则有
•
=1×
+0×2=
故答案为：
．
| AM |
| AD |
| DM |
| AD |
| 1 |
| 2 |
| AB |
| AN |
| AB |
| 1 |
| 2 |
| AD |
则有
| AB |
| 4 |
| 3 |
| AN |
| 2 |
| 3 |
| AM |
=
| 4 |
| 3 |
| 2 |
| 3 |
| 10 |
| 3 |
则有
| AB |
| AM |
| 10 |
| 3 |
| 10 |
| 3 |
故答案为：
| 10 |
| 3 |
点评：本题考查平面向量的数量积的坐标公式，考查向量的加法和减法运算，以及方程的思想方法，属于基础题．
练习册系列答案
相关题目
在△ABC中，已知sinA+cosA=
，则角A为（ ）
| 1 |
| 5 |
| A、锐角 | B、直角 |
| C、钝角 | D、锐角或钝角 |
在平面四边形ABCD中，AB=3，BC=4，∠ABC=90°，△ACD是正三角形，则| AC |
| BD |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|