题目内容

在平面四边形ABCD中，AB=3，BC=4，∠ABC=90°，△ACD是正三角形，则
AC
•
BD
的值为（　　）
A、-2
B、2
C、
7
2
D、-
7
2
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，建立直角坐标系．取AC的中点E，连接DE，BE．由A（0，3），C（4，0），可得E(2，
3
2
)．
由于
DE
⊥
AC
，可得
DE
•
AC
=0．利用
AC
•
BD
=
AC
•(
BE
+
ED
)=
AC
•
BE
即可得出．
解答： 解：如图所示，建立直角坐标系．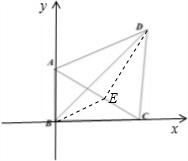
取AC的中点E，连接DE，BE．
∵A（0，3），C（4，0），∴E(2，
3
2
)．
∵
DE
⊥
AC
，∴
DE
•
AC
=0．
∴
AC
•
BD
=
AC
•(
BE
+
ED
)=
AC
•
BE

=(4，-3)•(2，
3
2
)
=8-
9
2

=
7
2
．
故选：C．
点评：本题考查了向量垂直与数量积的关系、数量积运算性质、向量的三角形法则，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
若A={x|3x-7＞0}，则∁RA=
 
．
设向量
a
=（sinx-1，1），
b
=（sinx+3，1），
c
=（-1，-2），
d
=（k，1），k∈R．
（Ⅰ）若x∈[-
π
2
，
π
2
]，且
a
∥（
b
+
c
），求x的值；
（Ⅱ）若存在x∈R，使得（
a
+
d
）⊥（
b
+
c
），求k的取值范围．
如图，已知在正方体ABCD-A1B1C1D1中，面对角线A1B、BC1的中点为E、F，求证：EF∥平面ABCD．
设D是不等式组
x+2y≤10
2x+y≥3
0≤x≤4
y≥1
表示的平面区域，则D中的点P（x，y）到直线x+y=10距离的最大值是
 
．
函数f（x）=cos2xcos
π
5
-2sinxcosxsin
6π
5
的递增区间是
 
．
在平行四边形ABCD中，M，N分别是CD，BC的中点，
AM
=(1，2) ， 
AN
=（3，1），则
AB
•
AM
=
 
．
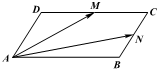
（Ⅰ） 如图，一个扇形OAB的面积是1cm2，它的周长是4cm，求圆心角的弧度数和弦长AB．
（Ⅱ） 已知f（x）=-sin2x+sinx+a，若1≤f（x）≤
17
4
对一切x∈R恒成立，求实数a的范围．
已知函数f（x）的定义域为{x|x∈R且x≠0}，对定义域内的任意x1，x2，都有f（x1•x2）=f（x1）+f（x2），且当x＞1时，f（x）＞0，
（1）求f（-1）的值；
（2）求证：f（x）是偶函数；
（3）求证：f（x）在（0，+∞）上是增函数；
（4）当f（16）=2时，解不等式f（x）+f（6x-5）＜1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网