题目内容
若动点P(x,y)满足
=|
x-
y-1|,则P点的轨迹应为( )
| (x-1)2+(y-2)2 |
| 3 |
| 5 |
| 4 |
| 5 |
| A、椭圆 | B、抛物线 | C、双曲线 | D、圆 |
考点:抛物线的定义,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:利用抛物线的定义即可得出.
解答:
解:动点P(x,y)满足
=|
x-
y-1|,
可知:动点P(x,y)到定点(1,2)与到定直线
x-
y-1=0的距离相等,其中定点不在定直线上.
因此P点的轨迹应为抛物线.
故选:B.
| (x-1)2+(y-2)2 |
| 3 |
| 5 |
| 4 |
| 5 |
可知:动点P(x,y)到定点(1,2)与到定直线
| 3 |
| 5 |
| 4 |
| 5 |
因此P点的轨迹应为抛物线.
故选:B.
点评:本题考查了抛物线的定义,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
“函数y=ax单调递减”是“lna<1”的什么条件.( )
| A、充分不必要 |
| B、必要不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
对于多项式P(x)=anxn+an-1xn-1+…+a1x+a0,分别韶算法和直接求和的方法求P(x0)时,可做乘法的次数分别为( )
| A、m,n | ||
B、n,
| ||
| C、n,n | ||
| D、2n+1,n |
等比数列{an}中,a1=2,a8=4,函数f(x)=x(x-a4)(x-a5),则[f′(0)]4=( )
| A、216 |
| B、212 |
| C、28 |
| D、24 |
已知数列{an}为等差数列,Sn为{an}的前n项和,且Sn=n2,则a10=( )
| A、17 | B、18 | C、19 | D、20 |
若tanα=3,则
的值等于( )
| 4sinα-2cosα |
| 5cosα+3sinα |
A、
| ||
B、
| ||
| C、1 | ||
D、-
|
已知函数f(x)=
(a>0,a≠1),数列{an}满足an=f(n)(n∈N*),且数列{an}是递增数列,则实数a的取值范围是( )
|
| A、[7,8) |
| B、(1,8) |
| C、(4,8) |
| D、(4,7) |
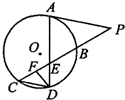 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,AE=12,ED=6,EF=4,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,AE=12,ED=6,EF=4,则PB=