题目内容
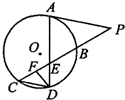如图，A是⊙O上的点，PC与⊙O相交于B、C两点，点D在⊙O上，CD∥AP，AD与BC交于E，F为CE上的点，若∠EDF=∠P，AE=12，ED=6，EF=4，则PB=考点：与圆有关的比例线段
专题：
分析：证明△DEF∽△PEA，根据三角形相似得到对应线段成比例，把比例式转化为乘积式，求出EP，再证明
=
，求出EC，利用相交弦定理求出EB，即可得出结论．
| EP |
| EC |
| AE |
| ED |
解答：
解：∵∠P=∠EDF，∠DEF=∠PEA，
∴△DEF∽△PEA．
∴DE：PE=EF：EA．
即EF•EP=DE•EA．
∵AE=12，ED=6，EF=4，
∴4•EP=72，
∴EP=18，
∵CD∥AP，
∴
=
，
∴EC=9，
∵弦AD、BC相交于点E，
∴DE•EA=CE•EB，
∴EB=8，
∴PB=EP-EB=10．
故答案为：10．
∴△DEF∽△PEA．
∴DE：PE=EF：EA．
即EF•EP=DE•EA．
∵AE=12，ED=6，EF=4，
∴4•EP=72，
∴EP=18，
∵CD∥AP，
∴
| EP |
| EC |
| AE |
| ED |
∴EC=9，
∵弦AD、BC相交于点E，
∴DE•EA=CE•EB，
∴EB=8，
∴PB=EP-EB=10．
故答案为：10．
点评：本题考查三角形相似的判断，考查相交弦定理，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
如图，AB是圆O的直径，过A、B的两条弦AC和BD相交于点P，若圆O的半径是2，那么AC•AP+BD•BP的值等于若动点P（x，y）满足
=|
x-
y-1|，则P点的轨迹应为（ ）
| (x-1)2+(y-2)2 |
| 3 |
| 5 |
| 4 |
| 5 |
| A、椭圆 | B、抛物线 | C、双曲线 | D、圆 |