题目内容
已知f1(x)=sinx+cosx,f2(x)=f1′(x),f3(x)=f2′(x)…fn(x)=fn-1′(x)(n∈N+,n≥2),记f1(
)+f2(
)+…+f2013(
)等于( )
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| A、1 | B、-1 | C、0 | D、-2 |
考点:导数的运算
专题:导数的概念及应用
分析:利用导数的运算法则,通过计算即可得出其周期性fn+4(x)=fn(x)进而即可得出答案.
解答:
解:∵f1(x)=sinx+cosx,fn+1(x)是fn(x)的导函数,
∴f2(x)=f1′(x)=cosx-sinx,f3(x)=f2′(x)=-sinx-cosx,f4(x)=-cosx+sinx,f5(x)=sinx+cosx,…,
∴fn+4(x)=fn(x),
∴f2013(x)=f503×4+1(x)=f1(x)=sinx+cosx.
∴f1(x)+f2(x)+f3(x)+f4(x)=sinx+cosx+cosx-sinx-sinx-cosx-cosx+sinx=0,
∴f1(
)+f2(
)+…+f2013(
)=f1(
)=sin
+cos
=1.
故选:A.
∴f2(x)=f1′(x)=cosx-sinx,f3(x)=f2′(x)=-sinx-cosx,f4(x)=-cosx+sinx,f5(x)=sinx+cosx,…,
∴fn+4(x)=fn(x),
∴f2013(x)=f503×4+1(x)=f1(x)=sinx+cosx.
∴f1(x)+f2(x)+f3(x)+f4(x)=sinx+cosx+cosx-sinx-sinx-cosx-cosx+sinx=0,
∴f1(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故选:A.
点评:熟练掌握导数的运算法则及得出其周期性fn+4(x)=fn(x)是解题的关键.

练习册系列答案
相关题目
函数f(x)=sin2(x-
)在[0,π]上的图象大致是( )
| π |
| 3 |
A、 |
B、 |
C、 |
D、 |
圆x2+y2-6x=0与圆x2+y2+8y+12=0的位置关系是( )
| A、相离 | B、相交 | C、外切 | D、内切 |
已知等差数列{an}中,am=k,ak=m,(m≠k),则am+k=( )
| A、m-k | B、m+k |
| C、-(m+k) | D、0 |
一个物体的运动方程是s=2t2+at+1,该物体在t=1时的瞬时速度为3,则a=( )
| A、1 | B、0 | C、-1 | D、7 |
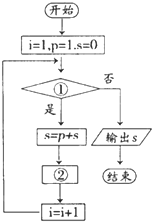 给出15个数:1,2,4,7,11,…,要计算这15个数的和,现给出解决该问题的程序框图(如图所示),那么框图中判断框①处和执行框②处应分别填入( )
给出15个数:1,2,4,7,11,…,要计算这15个数的和,现给出解决该问题的程序框图(如图所示),那么框图中判断框①处和执行框②处应分别填入( )| A、i≤16?; p=p+i-1 |
| B、i≤14?; p=p+i+1 |
| C、i≤15?; p=p+i+1 |
| D、i≤15?; p=p+i |
下列函数中与y=cosx奇偶性相同的是( )
| A、y=tanx |
| B、y=|sinx| |
| C、y=sinx |
| D、y=-sinx |