题目内容
设定义在R上的函数f(x)满足f(1)=1,f′(x)>
,其中f′(x)是f(x)的导函数,则不等式
f(x3)<
x3+
的解集为 .
| 1 |
| 3 |
f(x3)<
| 1 |
| 3 |
| 2 |
| 3 |
考点:导数的运算
专题:计算题,导数的概念及应用
分析:确定函数g(x)=f(x)-
x在R上是增函数,不等式f(x3)<
x3+
,转化为g(x3)<g(1),即可得出结论.
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
解答:
解:∵f′(x)>
,
∴[f(x)-
x]′>0,
∴函数g(x)=f(x)-
x在R上是增函数,
∴g(x3)=f(x3)-
x3;
∵不等式f(x3)<
x3+
,
∴g(x3)<
,
∵f(1)=1,g(1)=f(1)-
=
,
∴g(x3)<g(1),
∴x3<1,
∴x<1,
∴则不等式f(x3)<
x3+
的解集为(-∞,1).
故答案为:(-∞,1).
| 1 |
| 3 |
∴[f(x)-
| 1 |
| 3 |
∴函数g(x)=f(x)-
| 1 |
| 3 |
∴g(x3)=f(x3)-
| 1 |
| 3 |
∵不等式f(x3)<
| 1 |
| 3 |
| 2 |
| 3 |
∴g(x3)<
| 2 |
| 3 |
∵f(1)=1,g(1)=f(1)-
| 1 |
| 3 |
| 2 |
| 3 |
∴g(x3)<g(1),
∴x3<1,
∴x<1,
∴则不等式f(x3)<
| 1 |
| 3 |
| 2 |
| 3 |
故答案为:(-∞,1).
点评:本题考查导数知识的运用,考查函数的单调性,正确构建函数是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将函数f(x)=sinx图象所有的点向右移动
个单位长度,再将所得各点的横坐标缩短到原来的
倍(纵坐标不变),所得图象的函数解析式为( )
| π |
| 3 |
| 1 |
| 2 |
A、y=sin(
| ||||
B、y=sin(
| ||||
C、y=sin(2x-
| ||||
D、y=sin(2x-
|
如图所示是某一几何体的三视图,则它的体积为( )
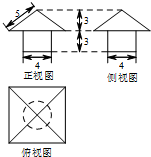

| A、16+12π |
| B、48+12π |
| C、64+12π |
| D、64+16π |
若曲线y=x2+ax+b在点(1,b)处的切线方程是x-y+1=0,则( )
| A、a=1,b=2 |
| B、a=-1,b=2 |
| C、a=1,b=-2 |
| D、a=-1,b=-2 |
 如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.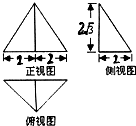 一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为
一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为