题目内容
在平面直角坐标系中,第一象限有系列圆On(n∈N*),所有圆均与x轴和直线
x-y=0相切,且任何相邻两圆外切:圆On的半径为rn,其中rn>rn+1>0,若圆O1的半径为r1=1,则rn等于 .
| 3 |
考点:圆的切线方程
专题:直线与圆
分析:由题意画出图形,利用三角形相似对应边成比例得到rn与rn+1的关系,进一步得到数列{rn}构成以1为首项,以
为公比的等比数列,则rn可求.
| 1 |
| 3 |
解答:
解:如图,

由相似三角形对应边成比例得,
=
,即3rn+1=rn,
∵r1=1≠0,
∴
=
,
则数列{rn}构成以1为首项,以
为公比的等比数列.
∴rn=(
)n-1.
故答案为:(
)n-1(n∈N*).

由相似三角形对应边成比例得,
| rn |
| rn+1 |
| 2rn |
| rn-rn+1 |
∵r1=1≠0,
∴
| rn+1 |
| rn |
| 1 |
| 3 |
则数列{rn}构成以1为首项,以
| 1 |
| 3 |
∴rn=(
| 1 |
| 3 |
故答案为:(
| 1 |
| 3 |
点评:本题考查了圆的切线方程,考查了等比数列的通项公式,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知a=0.3-0.2,b=log0.50.8,c=log0.53,那么a,b,c的大小关系是( )
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、a<c<b |
已知集合M={x|-2<x<1},N={x|-1<x<2},则M∩N=( )
| A、{x|-2<x<2} |
| B、{x|-1<x<2} |
| C、{x|-1<x<1} |
| D、{x|-2<x<1} |
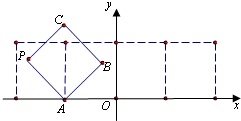 如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:
如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断: