题目内容

设f（x）=asin2x+bcos2x，其中a，b∈R，ab≠0．若f（x）≤|f(
π
6
)|对一切x∈R恒成立，则    
①f（-
π
12
）=0；      
②|f（
7π
12
）|＜|f(
π
5
)|；
③f（x）既不是奇函数也不是偶函数；  
④f（x）的单调递增区间是[kπ+
π
6
，kπ+
2π
3
]（k∈Z）；   
⑤存在经过点（a，b）的直线与函数f（x）的图象不相交．
以上结论正确的是（　　）
A、①②B、①②③
C、④⑤D、③④⑤
考点：命题的真假判断与应用,正弦函数的定义域和值域,正弦函数的单调性
专题：三角函数的图像与性质
分析：利用条件f（x）≤|f(
π
6
)|对一切x∈R恒成立，可知：当x=
π
6
时，f（x）取得最值，因此f(
π
6
)=±
a2+b2
，可得a=
3
b，可得f（x）．再利用三角函数的奇偶性、单调性等即可判断出．
解答： 解：∵f（x）≤|f(
π
6
)|对一切x∈R恒成立，∴f(
π
6
)=±
a2+b2
，∴asin
π
3
+bcos
π
3
=±
a2+b2
，
化为a=
3
b．
∴f（x）=2bsin(2x+
π
6
)．
①f（-
π
12
）=2bsin(-
π
12
×2+
π
6
)=0，正确；      
②|f（
7π
12
）|=|2bsin(
7π
6
+
π
6
)|=|2bsin
2π
3
|，|f(
π
5
)|=|2bsin(
2π
5
+
π
6
)|=|2bsin
17π
30
|．
∵
π
2
＜
17π
30
＜
2π
3
＜π，∴1＞sin
17π
30
＞sin
2π
3
＞0，
又b≠0，∴|f(
7π
12
)|＜|f(
π
5
)|；因此正确．
③∵f（-x）≠±f（x），∴f（x）既不是奇函数也不是偶函数，正确；  
④由-
π
2
+2kπ≤2x+
π
6
≤
π
2
+2kπ，解得-
π
3
+kπ≤x≤
π
6
+kπ（k∈Z）．
由
π
2
+2kπ≤2x+
π
6
≤
3π
2
+2kπ，解得
π
6
+kπ≤x≤
2π
3
+kπ（k∈Z）．
当b＜0时，f（x）的单调递增区间是[kπ+
π
6
，kπ+
2π
3
]（k∈Z）；  
当b＞0时，f（x）的单调递增区间是[-
π
3
+kπ，
π
6
+kπ]（k∈Z）．
因此函数f（x）的单调递增区间与b的正负有关，因此④不正确．
⑤∵f（x）≤|f(
π
6
)|=
a2+b2
，∴不存在经过点（a，b）的直线与函数f（x）的图象不相交，因此⑤不正确．
综上可知：只有①②③正确．
故选：B．
点评：本题综合考查了三角函数的图象与性质，考查了应用知识解决实际问题的能力，属于难题．
练习册系列答案
相关题目
椭圆C1以双曲线C2：
x2
4
-
y2
16
=1的实轴为短轴、虚轴为长轴，且与抛物线C3：y2=12x交于A，B两点．
（Ⅰ）求椭圆C1的方程及线段AB的长；
（Ⅱ）在C1与C3图象的公共区域内，是否存在一点P（x0，y0），使得C1的弦EF与C3的弦MN相互垂直平分于点P？若存在，求点P坐标，若不存在，说明理由．
在△ABC中，∠ABC=
π
3
，AB=2，BC=3，则sin∠BAC=
 
．
抛物线y2=4x的焦点到双曲线
x2
4
-y2=1的渐近线的距离是
 
．
复平面内有A，B，C三点，点A对应的复数为2+i，向量
BA
对应的复数为2+3i，向量
BC
对应的复数为3-i，则点C对应的复数
 
．
下列命题中正确的是（　　）
A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”
B、命题“?x∈R，x2-x≤0”的否定是“?x∈R，x2-x≥0”
C、命题“若x=y，则sinx=siny”的逆否命题为真命题
D、命题“p∧q为真”是命题“p∨q为真”的必要不充分条件
设集合A={x|x2-3x+4≥0}，集合B={x|log2x＞1}，则A∩∁RB=（　　）
A、（-∞，2）
B、（-∞，2]
C、（0，2）
D、（0，2]
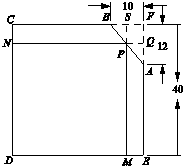有一块铁皮零件，它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE，其中AF长等于12cm，BF长等于10cm，如图所示．现在需要截取矩形铁皮，使得矩形相邻两边在CD，DE上．请问如何截取，可以使得到的矩形面积最大？（图中单位：cm）
已知f（x）=ax2+bx+3a+b是偶函数，且其定义域为[a-1，2a]，则y=f（x）的值域为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网