题目内容
已知函数f(x)=2sinx+1,是否存在实数a,使得函数y=(f(x)-1)2+2af(
-x)+
-6在区间[0,
]上的最大值是4?若存在,求出对应的a的值;若不存在,试说明理由.
| π |
| 2 |
| a |
| 2 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的最值
专题:存在型,分类讨论,三角函数的图像与性质
分析:假设存在实数a,然后应用同角三角函数的关系式和诱导公式对函数解析式化简整理,进而利用x的范围确定cosx的范围,根据二次函数的性质对a的范围进行分类讨论,求得函数的最大值,解出a,判断是否存在.
解答:
解:假设存在实数a,使得函数y=(f(x)-1)2+2af(
-x)+
-6
在区间[0,
]上的最大值是4,
则y=4sin2x+2a(2sin(
-x)+1)+
-6
即y=4sin2x+4acosx+
-6=-4(cos2x-acosx)+
-2
=-4(cosx-
)2+a2+
-2,
令cosx=t,则y=-4(t-
)2+a2+
-2,
∵0≤x≤
,∴0≤cosx≤1,即0≤t≤1,
当0≤
≤1时,即0≤a≤2,t=
时,y取最大值a2+
-2,且为4,解得a=
或-4(舍去);
当
>1时,即a>2,t=1时,y取最大值
-6,且为4,解得a=
,不符要求,舍去;
当
<0时,即a<0,t=0时,y取最大值
-2,且为4,解得a=
,不符要求,舍去.
故存在实数a,且为
,使得函数y=(f(x)-1)2+2af(
-x)+
-6在区间[0,
]上的最大值是4.
| π |
| 2 |
| a |
| 2 |
在区间[0,
| π |
| 2 |
则y=4sin2x+2a(2sin(
| π |
| 2 |
| a |
| 2 |
即y=4sin2x+4acosx+
| 5a |
| 2 |
| 5a |
| 2 |
=-4(cosx-
| a |
| 2 |
| 5a |
| 2 |
令cosx=t,则y=-4(t-
| a |
| 2 |
| 5a |
| 2 |
∵0≤x≤
| π |
| 2 |
当0≤
| a |
| 2 |
| a |
| 2 |
| 5a |
| 2 |
| 3 |
| 2 |
当
| a |
| 2 |
| 13a |
| 2 |
| 20 |
| 13 |
当
| a |
| 2 |
| 5a |
| 2 |
| 12 |
| 5 |
故存在实数a,且为
| 3 |
| 2 |
| π |
| 2 |
| a |
| 2 |
| π |
| 2 |
点评:本题主要考查三角函数的最值问题,考查二次函数型的最值问题,是动轴定区间,注意对动轴的讨论,同时考查三角函数的恒等变换应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.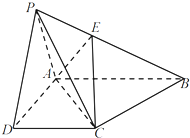 如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.
如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.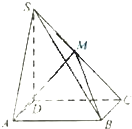 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=