题目内容
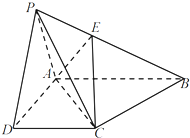 如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.
如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.(1)求证:AC⊥PB.
(2)在棱PB上取一点E,使直线PD∥平面ACE.
①求
| PE |
| EB |
②求证:二面角P-AC-D与E-AC-B大小相等.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(1)取AD中点O,由已知条件得PO⊥AD,PO⊥平面ABCD,连结OB,设OB∩AC=H,由已知条件推导出△BAO≌△ADC,由此能够证明AC⊥PB.
(Ⅱ)①连结BD交AC于F,连结EF,由已知条件推导出PD∥EF,由此能求出
的值.
②由已知条件推导出∠PHO,∠EHB分别是二面角P-AC-D与E-AC-B的平面角,由此能证明二面角P-AC-D与E-AC-B大小相等.
(Ⅱ)①连结BD交AC于F,连结EF,由已知条件推导出PD∥EF,由此能求出
| PE |
| EB |
②由已知条件推导出∠PHO,∠EHB分别是二面角P-AC-D与E-AC-B的平面角,由此能证明二面角P-AC-D与E-AC-B大小相等.
解答:
(1)证明:取AD中点O,则PO⊥AD,
由平面PAD⊥平面ABCD,得PO⊥平面ABCD,
连结OB,设OB∩AC=H,
∵AB=AD=2,DC=1,O是AD中点,AB⊥AD,DC⊥AD,
∴△BAO≌△ADC,
∴∠CAD=∠OBA,
∴∠CAD+∠AOB=∠OBA+∠AOB=90°,
∴∠AHO=90°,∴CA⊥PO,
∴CA⊥平面POB,
∴AC⊥PB.
(Ⅱ)①解:连结BD交AC于F,连结EF,
则EF是平面PBD与平面ACE的交线,
∵直线PD∥平面ACE,
∴PD∥EF,
∴
=
=
=
.
②证明:∵CA⊥面POB,
∴∠PHO,∠EHB分别是二面角P-AC-D与E-AC-B的平面角,
作EG⊥OB于G,在Rt△OAB中,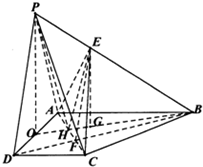
=
=
,
∴OH=
OB,HB=
OB,
又GB=
OB,
∴HG=HB-GB=
OB,
∴
=
=
=
,
∴tan∠PHO=tan∠EHG,
∴二面角P-AC-D与E-AC-B大小相等.
由平面PAD⊥平面ABCD,得PO⊥平面ABCD,
连结OB,设OB∩AC=H,
∵AB=AD=2,DC=1,O是AD中点,AB⊥AD,DC⊥AD,
∴△BAO≌△ADC,
∴∠CAD=∠OBA,
∴∠CAD+∠AOB=∠OBA+∠AOB=90°,
∴∠AHO=90°,∴CA⊥PO,
∴CA⊥平面POB,
∴AC⊥PB.
(Ⅱ)①解:连结BD交AC于F,连结EF,
则EF是平面PBD与平面ACE的交线,
∵直线PD∥平面ACE,
∴PD∥EF,
∴
| PE |
| EB |
| DF |
| FB |
| DC |
| AB |
| 1 |
| 2 |
②证明:∵CA⊥面POB,
∴∠PHO,∠EHB分别是二面角P-AC-D与E-AC-B的平面角,
作EG⊥OB于G,在Rt△OAB中,

| OH |
| HB |
| AO2 |
| AB2 |
| 1 |
| 4 |
∴OH=
| 1 |
| 5 |
| 4 |
| 5 |
又GB=
| 2 |
| 3 |
∴HG=HB-GB=
| 2 |
| 15 |
∴
| HG |
| OH |
| ||
|
| 2 |
| 3 |
| EG |
| PO |
∴tan∠PHO=tan∠EHG,
∴二面角P-AC-D与E-AC-B大小相等.
点评:本题考查异面直线垂直的证明,考查两条线段的比值的求法,考查两二面角相等的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: