题目内容
已知函数f(x)=2x-1的反函数为y=f-1(x),记g(x)=f-1(x-1).
(1)求函数y=2f-1(x)-g(x)的最小值;
(2)若函数F(x)=2f-1(x+m)-g(x)在区间[1,+∞)上是单调递增函数,求实数m的取值范围.
(1)求函数y=2f-1(x)-g(x)的最小值;
(2)若函数F(x)=2f-1(x+m)-g(x)在区间[1,+∞)上是单调递增函数,求实数m的取值范围.
考点:函数与方程的综合运用,函数单调性的判断与证明
专题:转化思想,函数的性质及应用
分析:(1)求出原函数的反函数,然后推出函数y=2f-1(x)-g(x)的表达式,即可求解其最小值;
(2)利用(1)函数的解析式,通过化简表达式,利用函数F(x)=2f-1(x+m)-g(x)在区间[1,+∞)上是单调递增函数,转化不等式,然后求实数m的取值范围.
(2)利用(1)函数的解析式,通过化简表达式,利用函数F(x)=2f-1(x+m)-g(x)在区间[1,+∞)上是单调递增函数,转化不等式,然后求实数m的取值范围.
解答:
解:(1)由f(x)=2x-1得x=log2(y+1),即f-1(x)=log2(x+1)(x>-1)
g(x)=f-1(x-1)=log2x,(x>0)
∴函数y=2f-1(x)-g(x)=2log2(x+1)-log2x=log2
=log2
=log2(x+
+2),
∵x>0,∴x+
+2≥4,当且仅当x=1时取等号,
∴函数y=2f-1(x)-g(x)的最小值为:log24=2.
(2)由f-1(x)=log2(x+1)(x>-1)得,
函数F(x)=2f-1(x+m)-g(x)=2log2(x+m+1)-log2x…(8分)
∴F(x)=log2
=log2[x+
+2(m+1)],
在区间[1,+∞)上是单调递增函数需满足:当x≥1时,x+m+1>0,即m>-2…(10分)
[|m+1|,+∞)⊆[1,+∞)…(12分),
即|m+1|≤1?-2≤m≤0,…(13分),
∴-2<m≤0…(14分)
g(x)=f-1(x-1)=log2x,(x>0)
∴函数y=2f-1(x)-g(x)=2log2(x+1)-log2x=log2
| (x+1)2 |
| x |
| x2+2x+1 |
| x |
| 1 |
| x |
∵x>0,∴x+
| 1 |
| x |
∴函数y=2f-1(x)-g(x)的最小值为:log24=2.
(2)由f-1(x)=log2(x+1)(x>-1)得,
函数F(x)=2f-1(x+m)-g(x)=2log2(x+m+1)-log2x…(8分)
∴F(x)=log2
| (x+m+1)2 |
| x |
| (m+1)2 |
| x |
在区间[1,+∞)上是单调递增函数需满足:当x≥1时,x+m+1>0,即m>-2…(10分)
[|m+1|,+∞)⊆[1,+∞)…(12分),
即|m+1|≤1?-2≤m≤0,…(13分),
∴-2<m≤0…(14分)
点评:本题考查函数恒成立问题,反函数以及对数函数基本不等式以及函数单调性的应用,考查转化思想以及分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若复数(m-1)+(m-2)i(m∈R)是纯虚数,则实数m等于( )
| A、0 | B、1 | C、2 | D、1或2 |
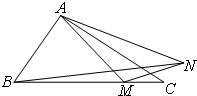 如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,
如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,