题目内容
将函数y=sin（6x+
）的图象上各点的横坐标伸长到原来的3倍，再向右平移
个单位，得到函数f（x）．
（1）写出f（x）的解析式
（2）求f（x）的对称中心．
| π |
| 4 |
| π |
| 8 |
（1）写出f（x）的解析式
（2）求f（x）的对称中心．
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（1）根据函数y=Asin（ωx+φ）的图象变换规律，得出结论．
（2）根据正弦函数的图象的对称性，求出f（x）的对称中心．
（2）根据正弦函数的图象的对称性，求出f（x）的对称中心．
解答：
解：（1）将函数y=sin（6x+
）的图象上各点的横坐标伸长到原来的3倍，可得函数y=sin（2x+
）的图象，
再向右平移
个单位，可得f（x）=sin[2（x-
）+
]=sin2x的图象．
（2）令2x=kπ，k∈z，求得x=
π，k∈z，
∴函数f（x）的对称中心(
，0)．
| π |
| 4 |
| π |
| 4 |
再向右平移
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
（2）令2x=kπ，k∈z，求得x=
| k |
| 2 |
∴函数f（x）的对称中心(
| kπ |
| 2 |
点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，属于中档题．
练习册系列答案
相关题目
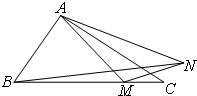如图，已知△ABC中，AB=1，AC=2，∠BAC=120°，点M是边BC上的动点，动点N满足∠MAN=30°，