Question

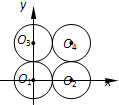如图，有4个半径都为1的圆，其圆心分别为O₁（0，0），O₂（2，0），O₃（0，2），O₄（2，2）．记集合M={⊙O_i|i=1，2，3，4}．若A，B为M的非空子集，且A中的任何一个圆与B中的任何一个圆均无公共点，则称 （A，B） 为一个“有序集合对”（当A≠B时，（A，B） 和 （B，A） 为不同的有序集合对），那么M中“有序集合对”（A，B） 的个数是（　　）

• A、2
• B、4
• C、6
• D、8

Answer 1

考点：圆与圆的位置关系及其判定

专题：直线与圆,集合

分析：分别求出A中有一个元素、A中有两个元素、A中有三个元素时，满足条件的集合B的个数，然后依次相加，能够求出结果．

解答： 解：不妨令A={⊙O₁}，B={⊙O₃}，满足“有序集合对”（A，B）的集合B的个数为2个，
令A={⊙O₂}，B={⊙O₄}，满足“有序集合对”（A，B）的集合B的个数为2个
当A是两个圆如：{⊙O₂，⊙O₃}，当A是三个圆如：{⊙O₁，⊙O₂，⊙O₄}，满足“有序集合对”（A，B）的集合B的个数为0，满足题意的“有序集合对”（A，B） 的个数是：4．
故选B．

点评：本题考查满足条件的集合的个数，解题时要认真审题，仔细解答，注意合理地进行分类．