题目内容
已知数列{an}满足an+2=
,若数列{an}中使得am=0的最小的m=60,求a1a2的值.
|
考点:数列递推式
专题:等差数列与等比数列
分析:由an+1≠0时,an+2=an-
,即an+2an+1-an+1an=-1,数列{an+1an}是公差为-1的等差数列,即可得出结论.
| 1 |
| an+1 |
解答:
解:由题意得a60=0,a61=0,
又an+1≠0时,an+2=an-
,即an+2an+1-an+1an=-1,
∴数列{an+1an}是公差为-1的等差数列,
∴a60a61=a1a2+(60-1)•(-1)=0,
∴a1a2=59.
又an+1≠0时,an+2=an-
| 1 |
| an+1 |
∴数列{an+1an}是公差为-1的等差数列,
∴a60a61=a1a2+(60-1)•(-1)=0,
∴a1a2=59.
点评:本题主要考查利用数列递推公式求数列的通项公式,构造数列{an+1an}是公差为-1的等差数列,是解决问题的关键,属于中档题.

练习册系列答案
相关题目
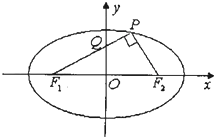 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
函数f(x)=
x2+(a-1)x+3在区间(-∞,4]上递减,则a的取值范围是( )
| 1 |
| 2 |
| A、[-3,+∞) |
| B、(-∞,-3] |
| C、(-∞,-3) |
| D、(-3,+∞) |