题目内容
若函数f(x)在R上是奇函数,且在(-1,0)上单调递增,且f(x+2)=-f(x).
(1)证明:f(x)的图象关于点(2k,0)中心对称,以及关于直线x=2k+1对称;
(2)讨论f(x)在区间(1,2)上的单调性.
(1)证明:f(x)的图象关于点(2k,0)中心对称,以及关于直线x=2k+1对称;
(2)讨论f(x)在区间(1,2)上的单调性.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)根据f(x+2)=-f(x)先求出函数的周期,再由奇函数的性质和f(x+2)=-f(x)得,函数的对称轴方程,再由f(x+2)=-f(x)和奇函数的周期知,函数关于(2k,0)(k∈Z)对称;
(2)根据条件和奇函数的单调性先得到函数在(0,1)上的单调性,再根据对称轴方程判断出在区间(1,2)上的单调性.
(2)根据条件和奇函数的单调性先得到函数在(0,1)上的单调性,再根据对称轴方程判断出在区间(1,2)上的单调性.
解答:
证明:(1)由题意得,则f(x+4)=-f(x+2)=f(x),
所以函数是以4为周期的周期函数,
因为f(x)为定义域为R的奇函数,f(x+2)=-f(x),
所以f(x+2)=f(-x),则f(x+4k+2)=f(-x),
所以函数f(x)的图象关于直线x=2k+1(k∈Z)对称,
因为f(x)为定义域为R的奇函数,
所以f(x)函数图象关于原点对称,
因为f(x)为周期函数,周期为4,且f(x+2)=-f(x),
所以f(x)函数图象关于点(2k,0)(k∈Z)对称;
(2)解:因为f(x)在R上是奇函数,且在(-1,0)上单调递增,
所以f(x)在(0,1)上单调递增,
由(1)知,函数f(x)的图象关于直线x=2k+1(k∈Z)对称,
所以函数f(x)的图象关于直线x=1对称,
则f(x)在区间(1,2)上的单调递减.
所以函数是以4为周期的周期函数,
因为f(x)为定义域为R的奇函数,f(x+2)=-f(x),
所以f(x+2)=f(-x),则f(x+4k+2)=f(-x),
所以函数f(x)的图象关于直线x=2k+1(k∈Z)对称,
因为f(x)为定义域为R的奇函数,
所以f(x)函数图象关于原点对称,
因为f(x)为周期函数,周期为4,且f(x+2)=-f(x),
所以f(x)函数图象关于点(2k,0)(k∈Z)对称;
(2)解:因为f(x)在R上是奇函数,且在(-1,0)上单调递增,
所以f(x)在(0,1)上单调递增,
由(1)知,函数f(x)的图象关于直线x=2k+1(k∈Z)对称,
所以函数f(x)的图象关于直线x=1对称,
则f(x)在区间(1,2)上的单调递减.
点评:本题考查了函数奇偶性、周期性、对称性和单调性的综合应用,关键是熟练掌握函数奇偶性、周期性、对称性的定义、性质,以及利用赋值法对等式进行灵活变形.

练习册系列答案
相关题目
数列{an}的前n项和为Sn,且Sn=2Sn+1+an2,a2=-1,则数列{an}的首项为( )
| A、1或-2 | B、±1 |
| C、±2 | D、-1或2 |
若执行如图所示的框图,输入x1=1,x2=2,x3=4,x4=8,则输出的数等于( )
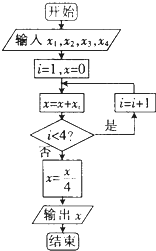

A、
| ||
B、
| ||
C、
| ||
| D、3 |