题目内容
已知点D(0,
),点P在圆C:x2+(y+
)2=16上,点,M在DP上,点N在CP上,且DM=MP.MN⊥DP.
(1)求点N的轨迹E的方程;
(2)是否存在点T(0,t),使过点T作圆O:x2+y2=1的切线l交曲线E与A、B两点,△AOB面积S取得最大值,若存在,求出S的最大值和相应的点T的坐标;若不存在,请说明理由.
| 3 |
| 3 |
(1)求点N的轨迹E的方程;
(2)是否存在点T(0,t),使过点T作圆O:x2+y2=1的切线l交曲线E与A、B两点,△AOB面积S取得最大值,若存在,求出S的最大值和相应的点T的坐标;若不存在,请说明理由.
考点:轨迹方程,直线与圆的位置关系
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由题意,NP=ND,NC+ND=CP=4,可得点N的轨迹E是以D,C为焦点的椭圆,且a=2,c=
,即可得到点M的轨迹方程;
(2)由过点T(0,t)作圆x2+y2=1的切线l交曲线C于A,B两点,得到|t|大于等于圆的半径1,分两种情况考虑:(i)当t=1时,确定出切线l为x=1,将x=1代入M得轨迹方程中,求出A和B的坐标,确定出此时|AB|的长,当t=-1时,同理得到|AB|的长;(ii)当|t|大于1时,设切线l方程为y=kx+t,将切线l的方程与圆方程联立,消去y得到关于x的一元二次方程,设A和B的坐标,利用根与系数的关系表示出两点横坐标之和与之积,再由切线l与圆相切,得到圆心到切线的距离d=r,利用点到直线的距离公式列出关系式,整理后得到k与t的关系式,然后利用两点间的距离公式表示出|AB|,将表示出的两根之和与两根之积,以及k与t的关系式代入,得到关于t的关系,利用基本不等式变形,得到|AB|的最大值,以及此时t的取值,而三角形AOB的面积等于AB与半径r乘积的一半来求,表示出三角形AOB的面积,将|AB|的最大值代入求出三角形AOB面积的最大值,以及此时T的坐标即可.
| 3 |
(2)由过点T(0,t)作圆x2+y2=1的切线l交曲线C于A,B两点,得到|t|大于等于圆的半径1,分两种情况考虑:(i)当t=1时,确定出切线l为x=1,将x=1代入M得轨迹方程中,求出A和B的坐标,确定出此时|AB|的长,当t=-1时,同理得到|AB|的长;(ii)当|t|大于1时,设切线l方程为y=kx+t,将切线l的方程与圆方程联立,消去y得到关于x的一元二次方程,设A和B的坐标,利用根与系数的关系表示出两点横坐标之和与之积,再由切线l与圆相切,得到圆心到切线的距离d=r,利用点到直线的距离公式列出关系式,整理后得到k与t的关系式,然后利用两点间的距离公式表示出|AB|,将表示出的两根之和与两根之积,以及k与t的关系式代入,得到关于t的关系,利用基本不等式变形,得到|AB|的最大值,以及此时t的取值,而三角形AOB的面积等于AB与半径r乘积的一半来求,表示出三角形AOB的面积,将|AB|的最大值代入求出三角形AOB面积的最大值,以及此时T的坐标即可.
解答:
解:(1)由题意,NP=ND,
∴NC+ND=CP=4,
∵点D(0,
),C(0,-
),
∴点N的轨迹E是以D,C为焦点的椭圆,且a=2,c=
,
∴b=1,
∴轨迹E的方程为x2+
=1;
(2)由题意知,|t|≥1,
(i)当t=1时,切线l的方程为y=1,点A、B的坐标分别为(-
,1),(
,1),
此时|AB|=
,当t=-1时,同理可得|AB|=
;
(ii)当|t|>1时,设切线l的方程为y=kx+t,k∈R,
代入椭圆方程,得(4+k2)x2+2ktx+t2-4=0③,
设A、B两点的坐标分别为(x1,y1),(x2,y2),
由③得:x1+x2=-
,x1x2=
,
又直线l与圆x2+y2=1相切,得
=1,即t2=k2+1,
∴|AB|=
,
又|AB|=
=
≤2,且当t=±
时,|AB|=2,
综上,|AB|的最大值为2,
依题意,圆心O到直线AB的距离为圆x2+y2=1的半径,
∴△AOB面积S=
|AB|×1≤1,
当且仅当t=±
时,△AOB面积S的最大值为1,相应的T的坐标为(0,-
)或(0,
).
∴NC+ND=CP=4,
∵点D(0,
| 3 |
| 3 |
∴点N的轨迹E是以D,C为焦点的椭圆,且a=2,c=
| 3 |
∴b=1,
∴轨迹E的方程为x2+
| y2 |
| 4 |
(2)由题意知,|t|≥1,
(i)当t=1时,切线l的方程为y=1,点A、B的坐标分别为(-
| ||
| 2 |
| ||
| 2 |
此时|AB|=
| 3 |
| 3 |
(ii)当|t|>1时,设切线l的方程为y=kx+t,k∈R,
代入椭圆方程,得(4+k2)x2+2ktx+t2-4=0③,
设A、B两点的坐标分别为(x1,y1),(x2,y2),
由③得:x1+x2=-
| 2kt |
| 4+k2 |
| t2-4 |
| 4+k2 |
又直线l与圆x2+y2=1相切,得
| |t| | ||
|
∴|AB|=
4
| ||
| t2+3 |
又|AB|=
4
| ||
| t2+3 |
4
| ||
|t|+
|
| 3 |
综上,|AB|的最大值为2,
依题意,圆心O到直线AB的距离为圆x2+y2=1的半径,
∴△AOB面积S=
| 1 |
| 2 |
当且仅当t=±
| 3 |
| 3 |
| 3 |
点评:此题考查了直线与圆相交的性质,以及动点的轨迹方程,涉及的知识有:直线与圆的交点,一元二次方程根与系数的关系,两点间的距离公式,点到直线的距离公式,基本不等式的运用,以及直线与圆相切时,圆心到直线的距离等于圆的半径的性质,利用了转化及分类讨论的思想,是一道综合性较强的试题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
数列{an}的前n项和为Sn,且Sn=2Sn+1+an2,a2=-1,则数列{an}的首项为( )
| A、1或-2 | B、±1 |
| C、±2 | D、-1或2 |
根据工作需要,现从4名女医生,a名男医生中选3名医生组成一个救援团队,其中a=
xdx,则团队中男、女医生都有的概率为( )
| ∫ | 1 0 |
| 5 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
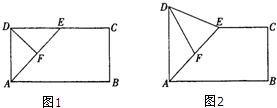 如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.
如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起. 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于