题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>1}\\{{2}^{|x|},x≤1}\end{array}\right.$,函数g(x)=f(x)-k有3个零点,则实数k的取值范围为( )| A. | (0,+∞) | B. | [1,+∞) | C. | (0,2) | D. | (1,2] |
分析 函数g(x)=f(x)-k有3个零点可化为函数f(x)与y=k有3个不同的交点,从而作图,结合图象求解即可.
解答 解:∵函数g(x)=f(x)-k有3个零点,
∴方程f(x)=k有且只有3个解,
∴函数f(x)与y=k有3个不同的交点,
∴作函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>1}\\{{2}^{|x|},x≤1}\end{array}\right.$与y=k的图象如下, ,
,
结合图象可知,
1<k≤2,
故选D.
点评 本题考查了函数的零点与函数的图象的交点个数的关系应用,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
12.函数f(x)=$\frac{x}{1-x}$+$\sqrt{x+1}$的定义域是( )
| A. | [-1,+∞) | B. | (-∞,-1) | C. | (-∞,+∞) | D. | [-1,1)∪(1,+∞) |
13.已知集合A={x|x2-5x+4≤0},B={-1,0,1,2,3},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
7.已知$tan(θ+\frac{π}{4})=\frac{1}{7}$且-$\frac{π}{2}$<θ<0,则sinθ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
11.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( )
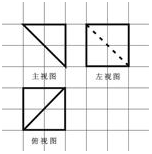

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
12.已知奇函数f(x)满足,x>0时,f(x)=x2-2x;则x<0时,f(x)的解析式为( )
| A. | -x2-2x | B. | -x2+2x | C. | x2-2x | D. | x2+2x |