题目内容
12.函数f(x)=$\frac{x}{1-x}$+$\sqrt{x+1}$的定义域是( )| A. | [-1,+∞) | B. | (-∞,-1) | C. | (-∞,+∞) | D. | [-1,1)∪(1,+∞) |
分析 函数f(x)=$\frac{x}{1-x}$+$\sqrt{x+1}$有意义,只需1-x≠0,且1+x≥0,解不等式即可得到所求定义域.
解答 解:函数f(x)=$\frac{x}{1-x}$+$\sqrt{x+1}$有意义,
只需1-x≠0,且1+x≥0,
解得x≥-1且x≠1,
则定义域为[-1,1)∪(1,+∞).
故选:D.
点评 本题考查函数定义域的求法,注意运用分式分母不为0,偶次根式被开方数非负,属于基础题.

练习册系列答案
相关题目
3.集合M={x∈N+|-$\sqrt{3}$≤x≤$\sqrt{3}}$},则下列说法正确的是( )
| A. | $\sqrt{3}∈M$ | B. | 1∉M | C. | M是空集 | D. | 该集合是有限集 |
2.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>1}\\{{2}^{|x|},x≤1}\end{array}\right.$,函数g(x)=f(x)-k有3个零点,则实数k的取值范围为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,2) | D. | (1,2] |
 如图,过圆内接四边形ABCD的顶点C引切线MN,AB为圆的直径.
如图,过圆内接四边形ABCD的顶点C引切线MN,AB为圆的直径.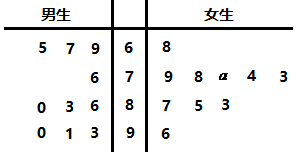 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).