Question

11．如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的体积为（　　）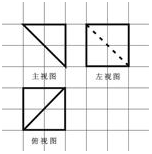　

• A． $\frac{8}{3}$
• B． $\frac{4}{3}$
• C． 4$\sqrt{3}$
• D． 2$\sqrt{3}$

Answer 1

分析 由已知可得该几何体是一个以正方体对角面为底面的四棱锥，进而得到答案．

解答 解：由已知可得该几何体是一个以正方体对角面为底面的四棱锥，
由正方体的棱长为2，
故四棱锥的底面面积S=2×2$\sqrt{2}$=4$\sqrt{2}$，
四棱锥的高h=$\sqrt{2}$，
故四棱锥的体积V=$\frac{1}{3}Sh$=$\frac{8}{3}$，
故选：A

点评 本题考查的知识点是棱锥的体积和表面积，空间几何体的三视图，根据已知分析出几何体的形状，是解答的关键．