题目内容
14.下列各组中的两个函数是同一函数的为( )①y=$\frac{(x+3)(x-5)}{x+3}$,y=x-5,
②y=x2-1,y=$\sqrt{({x}^{2}-1)^{2}}$;
③y=x2-1,y=$\root{3}{({x}^{2}-1)^{3}}$,
④y=($\sqrt{2x-5}$)2,y=2x-5.
| A. | ① | B. | ② | C. | ②④ | D. | ③ |
分析 分别判断两个函数的定义域和对应法则是否相同即可.
解答 解:对于①,y=$\frac{(x+3)(x-5)}{x+3}$=x-5(x≠-3),与y=x-5(x∈R)的定义域不相同,不是同一函数.
对于②,y=x2-1(x∈R),与y=$\sqrt{{{(x}^{2}-1)}^{2}}$=|x2-1|(x∈R)的对应关系不相同,不是同一函数.
对于③,y=x2-1(x∈R),与y=$\root{3}{{{(x}^{2}-1)}^{3}}$=x2-1(x∈R)的定义域和对应法则相同,是同一函数.
对于④,y=${(\sqrt{2x-5})}^{2}$=2x-5(x≥$\frac{5}{2}$),与y=2x-5(x∈R)的定义域不相同,不是同一函数.
综上,是同一函数的为③.
故选:D.
点评 本题主要考查了判断两个函数是否为同一函数的应用问题,是基础题目.

练习册系列答案
相关题目
5.若复数z=2+i,则$\frac{z•\overline{z}}{{i}^{2}}$等于( )
| A. | 5 | B. | -5 | C. | 5i | D. | -5i |
2.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>1}\\{{2}^{|x|},x≤1}\end{array}\right.$,函数g(x)=f(x)-k有3个零点,则实数k的取值范围为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,2) | D. | (1,2] |
9.若tanα=2,则cos2α-sin2α的值为( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
19. 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )| A. | i≤4 | B. | i≤5 | C. | i≤6 | D. | i≤7 |
3.在△ABC中,AB=AC=2,BC•cos(π-A)=1,则cosA的值所在区间是( )
| A. | (-0.5,-0.4) | B. | (-0.4,-0.3) | C. | (0.4,0.6) | D. | (0.8,0.9) |
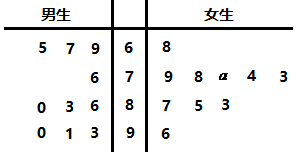 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).