题目内容
13.已知集合A={x|x2-5x+4≤0},B={-1,0,1,2,3},则A∩B=( )| A. | {-1,0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
分析 利用交集性质直接求解.
解答 解:∵集合A={x|x2-5x+4≤0}={x|1≤x≤4},
B={-1,0,1,2,3},
∴A∩B={1,2,3}.
故选:C.
点评 本题考查交集运算,是基础题,解题时要认真审题,注意交集的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.集合M={x∈N+|-$\sqrt{3}$≤x≤$\sqrt{3}}$},则下列说法正确的是( )
| A. | $\sqrt{3}∈M$ | B. | 1∉M | C. | M是空集 | D. | 该集合是有限集 |
5.若复数z=2+i,则$\frac{z•\overline{z}}{{i}^{2}}$等于( )
| A. | 5 | B. | -5 | C. | 5i | D. | -5i |
2.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>1}\\{{2}^{|x|},x≤1}\end{array}\right.$,函数g(x)=f(x)-k有3个零点,则实数k的取值范围为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,2) | D. | (1,2] |
3.在△ABC中,AB=AC=2,BC•cos(π-A)=1,则cosA的值所在区间是( )
| A. | (-0.5,-0.4) | B. | (-0.4,-0.3) | C. | (0.4,0.6) | D. | (0.8,0.9) |
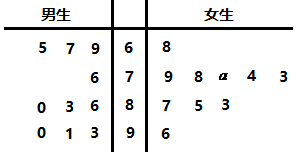 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).