题目内容
9.已知数列1,$\sqrt{3}$,$\sqrt{5}$,$\sqrt{7}$,…,$\sqrt{2n-1}$,…则3$\sqrt{5}$是它的第23项.分析 根据题意,列方程$\sqrt{2n-1}$=3$\sqrt{5}$,解方程即可.
解答 解:根据题意,令$\sqrt{2n-1}$=3$\sqrt{5}$,
两边平方得2n-1=45,
解得n=23.
故答案为:23.
点评 本题考查了数列的概念与通项公式的应用问题,是基础题.

练习册系列答案
相关题目
19.$\overrightarrow a$=(-1,-5,-2),$\overrightarrow b$=(x,2,x+2),若$\overrightarrow a⊥\overrightarrow b$,则x=( )
| A. | 0 | B. | -6 | C. | $-\frac{14}{3}$ | D. | ±6 |
20.在${({\sqrt{x}+\frac{3}{x}})^n}$的展开式中,各二项式系数之和为64,则展开式中常数项为( )
| A. | 135 | B. | 105 | C. | 30 | D. | 15 |
17.已知实数x,y满足x2+4y2≤4,则|x+2y-4|+|3-x-y|的最大值为( )
| A. | 6 | B. | 12 | C. | 13 | D. | 14 |
1.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{FQ}=-4\overrightarrow{FP}$,则|QF|=( )
| A. | 35 | B. | $\frac{5}{2}$ | C. | 20 | D. | 3 |
18.设复数z满足$\overline{z}$=|1-i|+i(i为虚数单位),则复数z为( )
| A. | $\sqrt{2}$-i | B. | $\sqrt{2}$+i | C. | 1 | D. | -1-2i |
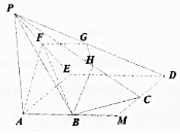 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.