题目内容
18.设复数z满足$\overline{z}$=|1-i|+i(i为虚数单位),则复数z为( )| A. | $\sqrt{2}$-i | B. | $\sqrt{2}$+i | C. | 1 | D. | -1-2i |
分析 利用复数的模的计算公式、共轭复数的定义即可得出.
解答 解:复数z满足$\overline{z}$=|1-i|+i=$\sqrt{2}$+i,则复数z=$\sqrt{2}$-i.
故选:A.
点评 本题考查了复数的模的计算公式、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
8.已知双曲线的焦点到渐进线的距离等于实半轴长,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
10.命题p:?x<0,x2≥2x,则命题¬p为( )
| A. | ?x0<0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | B. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | ||
| C. | ?x0<0,x${\;}_{0}^{2}$<2${\;}^{{x}_{0}}$ | D. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ |
7.已知数列{an)中,a1=2,an=1-$\frac{1}{{a}_{n-1}}$(n≥2),则a2017等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -1 | D. | 2 |
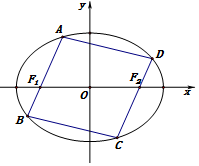 已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,
已知椭圆E的中心在原点,焦点F1、F2在x轴上,离心率为$\frac{1}{2}$,在椭圆E上有一动点A与F1、F2的距离之和为4,