题目内容
1．已知抛物线C：y2=8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若$\overrightarrow{FQ}=-4\overrightarrow{FP}$，则|QF|=（ ）| A． | 35 | B． | $\frac{5}{2}$ | C． | 20 | D． | 3 |
分析 抛物线C：y2=8x的焦点为F（2，0），设P（-2，t），Q（x，y）．利用$\overrightarrow{FQ}=-4\overrightarrow{FP}$，可得（-4）（-4，t）=4（x-2，y），解得（x，y），代入y2=8x可得t2=128，再利用两点之间的距离公式即可得出．
解答 解：抛物线C：y2=8x的焦点为F（2，0），设P（-2，t），Q（x，y）．
∵$\overrightarrow{FQ}=-4\overrightarrow{FP}$，可得（-4）•（-4，t）=（x-2，y），
解得$\left\{\begin{array}{l}{x=18}\\{y=-4t}\end{array}\right.$
由抛物线的定义知|QF|=x+$\frac{p}{2}$=18+2=20
故选：C
点评 本题考查抛物线的定义和性质，考查向量知识的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
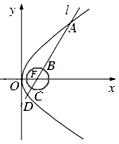如图，已知抛物线y2=4x的焦点为F，直线l过F且依次交抛物线及圆（x-1）2+y2=$\frac{1}{4}$于点A，B，C，D四点，则9|AB|+4|CD|的最小值为$\frac{37}{2}$．
如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点，且椭圆C过点P（2，1），若直线l与直线OP平行且与椭圆C相交于点A，B．
16．下列函数中，在其定义域内既是奇函数又是增函数的为（ ）
| A． | y=lnx3 | B． | y=-x2 | C． | y=-$\frac{1}{x}$ | D． | y=x|x| |
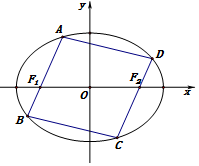已知椭圆E的中心在原点，焦点F1、F2在x轴上，离心率为$\frac{1}{2}$，在椭圆E上有一动点A与F1、F2的距离之和为4，
10．命题p：?x＜0，x2≥2x，则命题￢p为（ ）
| A． | ?x0＜0，x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | B． | ?x0≥0，x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | ||
| C． | ?x0＜0，x${\;}_{0}^{2}$＜2${\;}^{{x}_{0}}$ | D． | ?x0≥0，x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ |
