题目内容
14.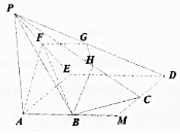 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.(1)求证:AB∥FG;
(2)若PA⊥平面ABCDE,且PA=AE,求平面PCD与平面ABF所成角(锐角)的余弦值,并求线段PH的长.
分析 (1)推导出AB∥DE,从而AB∥平面PDE,由此能证明AB∥FG.
(2)以A为原点,分别以AM,AE,AP为x,y,z的正半轴建立空间直角坐标系,利用向量法能求出平面PCD与平面ABF所成角(锐角)的余弦值和PH的长.
解答 证明:(1)在正方形AMDE中,∵B是AM的中点,∴AB∥DE,
∵AB?平面PDE,DE?平面PDE,∴AB∥平面PDE,
∵AB?平面ABF,且面ABF∩平面PDE=FG,
∴AB∥FG.
解:(2)∵PA⊥底面ABCDE,∴PA⊥AB,PA⊥AE,
∴以A为原点,分别以AM,AE,AP为x,y,z的正半轴建立空间直角坐标系,
则A(0,0,0),B(1,0,0),C(2,1,0),D(2,2,0),P(0,0,2),F(0,1,1),
设平面ABF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PC}=y=0}\\{\overrightarrow{n}•\overrightarrow{PD}=x-z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(0,-1,1),
设平面PCD的法向量为$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PC}=b=0}\\{\overrightarrow{m}•\overrightarrow{PD}=a-c=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,0,1),
设平面PCD与平面ABF所成角(锐角)为θ,
则cosθ=$\frac{|\overrightarrow{n}•\overrightarrow{m}|}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{1}{2}$,
∴平面PCD与平面ABF所成角(锐角)的余弦值为$\frac{1}{2}$.
设点H(μ,v,w),∵点H 在棱PC上,设$\overrightarrow{PH}=λ\overrightarrow{PC}$(0<λ<1),
则(μ,v,w)=λ(2,1,-2),∴μ=2λ,v=λ,w=2-2λ,
∵平面ABF的法向量为$\overrightarrow{n}$=(0,-1,1),
∴$\overrightarrow{n}•\overrightarrow{AH}$=-λ+2-2λ=0,解得$λ=\frac{2}{3}$,
∴H($\frac{4}{3},\frac{2}{3},\frac{2}{3}$),∴PH=$\sqrt{(\frac{4}{3})^{2}+(\frac{2}{3})^{2}+(2-\frac{2}{3})^{2}}$=2.
点评 本题考查线线平行的证明,考查二面角的余弦值的求法,考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | p=4 | B. | p=8 | C. | p=4或p=8 | D. | p=2或p=4 |

| A. | 8 | B. | 18 | C. | 26 | D. | 80 |
| A. | (-2,+∞) | B. | (-2,2) | C. | (-∞,-2) | D. | (-∞,+∞) |