题目内容
20.在${({\sqrt{x}+\frac{3}{x}})^n}$的展开式中,各二项式系数之和为64,则展开式中常数项为( )| A. | 135 | B. | 105 | C. | 30 | D. | 15 |
分析 由题意可得:2n=64,解得n,再利用通项公式即可得出.
解答 解:由题意可得:2n=64,解得n=6.
∴$(\sqrt{x}+\frac{3}{x})^{6}$的通项公式:Tr+1=${∁}_{6}^{r}(\sqrt{x})^{6-r}(\frac{3}{x})^{r}$=${3}^{r}{∁}_{6}^{r}$${x}^{3-\frac{3r}{2}}$,
令3-$\frac{3r}{2}$=0,解得r=2.
∴展开式中常数项为${3}^{2}•{∁}_{6}^{2}$=135.
故选:A.
点评 本题考查了二项式定理的性质及其应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
10. 某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )
某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )
 某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )
某实心钢质工件的三视图如图所示,其中侧视图为等腰三角形,俯视图是一个半径为3的半圆,现将该工件切削加工成一个球体,则该球体的最大体积为( )| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
8.已知双曲线的焦点到渐进线的距离等于实半轴长,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
10.命题p:?x<0,x2≥2x,则命题¬p为( )
| A. | ?x0<0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | B. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ | ||
| C. | ?x0<0,x${\;}_{0}^{2}$<2${\;}^{{x}_{0}}$ | D. | ?x0≥0,x${\;}_{0}^{2}$≥2${\;}^{{x}_{0}}$ |
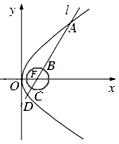 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=$\frac{1}{4}$于点A,B,C,D四点,则9|AB|+4|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆(x-1)2+y2=$\frac{1}{4}$于点A,B,C,D四点,则9|AB|+4|CD|的最小值为$\frac{37}{2}$. 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.