题目内容
已知函数f（x）=
，其中a∈R
（Ⅰ）若a=0，求函数f（x）的极值；
（Ⅱ）当a＞1时，试确定函数f（x）的单调区间．
| ex+1 |
| ax2+4x+4 |
（Ⅰ）若a=0，求函数f（x）的极值；
（Ⅱ）当a＞1时，试确定函数f（x）的单调区间．
考点：利用导数研究函数的单调性,利用导数研究函数的极值
专题：导数的概念及应用
分析：（Ⅰ）利用导数求极值；
（Ⅱ）利用导数求函数的单调区间．
（Ⅱ）利用导数求函数的单调区间．
解答：
解：（Ⅰ）由a=0得f（x）=
，∴f′（x）=
=
∴由f′（x）=0得x=0，又∵x＜0时，f′（x）＜0；x＞0时，f′（x）＞0
∴x=0时，f（x）有极小值为
．
（Ⅱ）当a＞1时，f′（x）=
∴f′（x）=0的两根为0，
．
∴当1＜a＜2时，由f′（x）＞0得x＜
或x＞0，故f（x）的递增区间为（-∞，
），（0，+∞）
由f′（x）＜0得
＜x＜0，故f（x）的递减区间为（
，0）；
当a≥2时，由f′（x）＞0得x＞
或x＜0，故f（x）的递增区间为（
，+∞），（-∞，0）
由f′（x）＜0得0＜x＜
，故f（x）的递减区间为（0，
）；
| ex+1 |
| 4x+4 |
| ex+1(4x+4)-4ex+1 |
| 16(x+1)2 |
| xex+1 |
| 4(x+1)2 |
∴由f′（x）=0得x=0，又∵x＜0时，f′（x）＜0；x＞0时，f′（x）＞0
∴x=0时，f（x）有极小值为
| e |
| 4 |
（Ⅱ）当a＞1时，f′（x）=
| x(ax+4-2a)ex+1 |
| (ax2+4x+4)2 |
∴f′（x）=0的两根为0，
| 2a-4 |
| a |
∴当1＜a＜2时，由f′（x）＞0得x＜
| 2a-4 |
| a |
| 2a-4 |
| a |
由f′（x）＜0得
| 2a-4 |
| a |
| 2a-4 |
| a |
当a≥2时，由f′（x）＞0得x＞
| 2a-4 |
| a |
| 2a-4 |
| a |
由f′（x）＜0得0＜x＜
| 2a-4 |
| a |
| 2a-4 |
| a |
点评：考查学生运用导数求函数的极值及单调区间的方法，解题时注意对a进行分类讨论．
练习册系列答案
相关题目
如图，在三棱锥A-BCD中，BA=BD，AD⊥CD，E、F分别为AC、AD的中点．
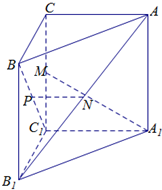如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，且∠ACB=90°，∠BAC=30°，BC=1，AA1=
已知椭圆C：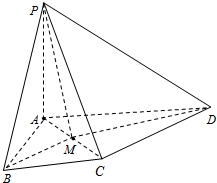
如图所示，PA⊥平面ABCD，△ABC为等边三角形，AP=AB，AC⊥CD，M为AC的中点． 
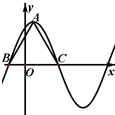函数f（x）=2