题目内容
已知f(x)=x|x-a|+2x-3,其中a∈R
(1)当a=4,2≤x≤5时,求函数f(x)的最大值和最小值,并写出相应的x的值.
(2)若f(x)在R上恒为增函数,求实数a的取值范围.
(1)当a=4,2≤x≤5时,求函数f(x)的最大值和最小值,并写出相应的x的值.
(2)若f(x)在R上恒为增函数,求实数a的取值范围.
考点:函数单调性的性质
专题:函数的性质及应用
分析:(1)化为分段函数,利用函数的增减性求得最值;
(2)通过讨论a的取值,化为分段函数后由函数的单调性列出不等式求得.
(2)通过讨论a的取值,化为分段函数后由函数的单调性列出不等式求得.
解答:
解;(1)∵f(x)=x|x-a|+2x-3,
∴当a=4时,f(x)=x|x-4|+2x-3=
;
作图如下:
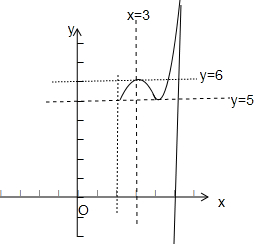
由图知,当x=5时,f(x)max=f(5)=52-2×5-3=12;
当x=2或4时,f(x)min=f(2)=f(4)=-22+6×2-3=5,
(2)f(x)=
,
∵f(x)在R上恒为增函数,
∴
,解得-2≤a≤2.
∴实数a的取值范围是[-2,2].
∴当a=4时,f(x)=x|x-4|+2x-3=
|
作图如下:

由图知,当x=5时,f(x)max=f(5)=52-2×5-3=12;
当x=2或4时,f(x)min=f(2)=f(4)=-22+6×2-3=5,
(2)f(x)=
|
∵f(x)在R上恒为增函数,
∴
|
∴实数a的取值范围是[-2,2].
点评:本题考查学生对含绝对值的函数的处理方法,以及分段函数的单调性的判断与运用能力,结合图象理解更好.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知椭圆C:
已知椭圆C: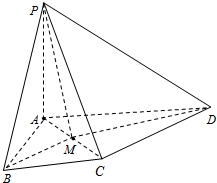 如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.
如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.