题目内容
已知椭圆中心在原点,焦点在x轴上,离心率e=
,过椭圆的右焦点且垂直于长轴的弦长为
.
(1)求椭圆的标准方程;
(2)A为椭圆左顶点,P,Q为椭圆上异于A的任意两点,若
⊥
,求证:直线PQ过定点并求出定点坐标.
| ||
| 2 |
| 2 |
(1)求椭圆的标准方程;
(2)A为椭圆左顶点,P,Q为椭圆上异于A的任意两点,若
| AP |
| AQ |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)首先,设该椭圆的标准方程为:
+
=1(a>b>0),然后,利用待定系数法,建立关系式,利用离心率和通径长建立方程组,求解a和b即可;
(2)首先,设直线PQ:x=my+n,然后,设P(x1,y1),Q(x2,y2),然后,联立方程组,消去y,结合
⊥
,建立等式,求解定点即可.
| x2 |
| a2 |
| y2 |
| b2 |
(2)首先,设直线PQ:x=my+n,然后,设P(x1,y1),Q(x2,y2),然后,联立方程组,消去y,结合
| AP |
| AQ |
解答:
(1)设椭圆的标准方程为:
+
=1(a>b>0),
则e=
=
=
①
∵
=
②
联立①②,解得
a=
,b=1
∴椭圆的标准方程为
+y2=1;
(2)设PQ:x=my+n,P(x1,y1),Q(x2,y2),
代入椭圆方程得(m2+2)y2+2mny+n2-2=0,
∴△≥0,y1+y2=
,y1y2=
,
又
⊥
,
∴(x1+
)(x2+
)+y1y2=0⇒(my1+n+
)(my2+n+
)+y1y2=0,⇒(1+m2)y1y2+m(n+
)y1y2+(n+
)2=0,
(1+m2)
+m(n+
)
+(n+
)2=0,
化简得:3n2+4
n+2=0⇒n=-
或n=-
(舍去)
∴直线PQ:x=my-
,即过定点(-
,0).
| x2 |
| a2 |
| y2 |
| b2 |
则e=
| c |
| a |
| ||
| a |
| ||
| 2 |
∵
| 2b2 |
| a |
| 2 |
联立①②,解得
a=
| 2 |
∴椭圆的标准方程为
| x2 |
| 2 |
(2)设PQ:x=my+n,P(x1,y1),Q(x2,y2),
代入椭圆方程得(m2+2)y2+2mny+n2-2=0,
∴△≥0,y1+y2=
| -2mn |
| m2+2 |
| n2-2 |
| m2+2 |
又
| AP |
| AQ |
∴(x1+
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(1+m2)
| n2-2 |
| m2+2 |
| 2 |
| -2mn |
| m2+2 |
| 2 |
化简得:3n2+4
| 2 |
| ||
| 3 |
| 2 |
∴直线PQ:x=my-
| ||
| 3 |
| ||
| 3 |
点评:本题重点考查了椭圆的标准方程的求解、椭圆的几何性质、直线与椭圆的位置关系等知识,属于综合性题目,本题需要注意直线方程的设法,直线过定点问题的处理思路和方法等,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
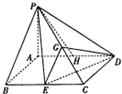 已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=
已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=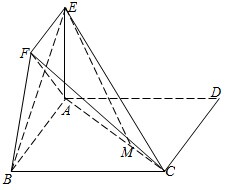 如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,
如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,