题目内容
已知函数f(x)为反比例函数,且图象经过(-1,2),g(x)=x2-2x.
(1)求函数f[g(x)]的解析式与定义域;
(2)求函数f[g(x)]的值域;
(3)判断并证明函数f[g(x)]在区间(2,+∞)上的单调性.
(1)求函数f[g(x)]的解析式与定义域;
(2)求函数f[g(x)]的值域;
(3)判断并证明函数f[g(x)]在区间(2,+∞)上的单调性.
考点:函数单调性的判断与证明
专题:计算题,证明题,函数的性质及应用
分析:(1)代入点求出f(x)的解析式,从而求函数f[g(x)]的解析式与定义域;(2)分母不能为0;(3)先判断,后用定义法证明.
解答:
解:(1)设f(x)=
,则2=
,解得k=-2.
则f(x)=-
,
则f[g(x)]=
,
由x2-2x≠0解得函数f[g(x)]的定义域为
{x|x≠0且x≠2}.
(2)∵x2-2x=(x-1)2-1≥-1且x2-2x≠0;
则
<0或
≥2;
即函数f[g(x)]的值域为(-∞,0)∪[2,+∞).
(3)f[g(x)]在区间(2,+∞)上的单调递增,证明如下:
任取x1,x2∈(2,+∞),且x1<x2,则
f(x1)-f(x2)=
-
=-
,
∵2<x1<x2,
∴-
<0,
即:f(x1)<f(x2);
∴f[g(x)]在区间(2,+∞)上的单调递增.
| k |
| x |
| k |
| -1 |
则f(x)=-
| 2 |
| x |
则f[g(x)]=
| -2 |
| x2-2x |
由x2-2x≠0解得函数f[g(x)]的定义域为
{x|x≠0且x≠2}.
(2)∵x2-2x=(x-1)2-1≥-1且x2-2x≠0;
则
| -2 |
| x2-2x |
| -2 |
| x2-2x |
即函数f[g(x)]的值域为(-∞,0)∪[2,+∞).
(3)f[g(x)]在区间(2,+∞)上的单调递增,证明如下:
任取x1,x2∈(2,+∞),且x1<x2,则
f(x1)-f(x2)=
| -2 |
| x12-2x1 |
| -2 |
| x22-2x2 |
=-
| 2(x2-x1)(x2+x1-2) |
| x1x2(x1-2)(x2-2) |
∵2<x1<x2,
∴-
| 2(x2-x1)(x2+x1-2) |
| x1x2(x1-2)(x2-2) |
即:f(x1)<f(x2);
∴f[g(x)]在区间(2,+∞)上的单调递增.
点评:本题综合考查了函数的定义及其基本性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
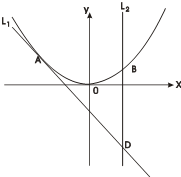 已知A(-1,2)为曲线C:y=2x2上的点,直线l1过点A,且与曲线C相切,
已知A(-1,2)为曲线C:y=2x2上的点,直线l1过点A,且与曲线C相切,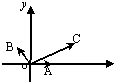 如图所示,|
如图所示,|