题目内容
5.已知函数f(x)=$\frac{1}{3}$x3-kx2+2x,x∈R,k∈R.①若f′(-1)=1,则k的值为-1.
②若函数f(x)在区间(1,2)内存在2个极值点,则k的取值范围是$\sqrt{2}<k<\frac{3}{2}$.
分析 ①求出原函数的导函数,再由f′(-1)=1列式求得k值;
②把函数f(x)在区间(1,2)内存在2个极值点,转化为函数f′(x)=x2-2kx+2在区间(1,2)内存在2个零点,即方程x2-2kx+2=0在区间(1,2)内有两个不同根,由一元二次方程根的分布得关于k的不等式组求解.
解答 解:①∵f(x)=$\frac{1}{3}$x3-kx2+2x,
∴f′(x)=x2-2kx+2,
由f′(-1)=(-1)2+2k+2=1,得k=-1;
②∵函数f(x)在区间(1,2)内存在2个极值点,
∴函数f′(x)=x2-2kx+2在区间(1,2)内存在2个零点,
即方程x2-2kx+2=0在区间(1,2)内有两个不同根.
∴$\left\{\begin{array}{l}{△=4{k}^{2}-8>0}\\{1<-\frac{-2k}{2}<2}\\{{1}^{2}-2k×1+2>0}\\{{2}^{2}-2k×2+2>0}\end{array}\right.$,解得:$\sqrt{2}<k<\frac{3}{2}$.
故答案为:①-1;②$\sqrt{2}<k<\frac{3}{2}$.
点评 本题考查利用导数研究函数的单调性,训练了利用导数求函数的极值,体现了数学转化思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知A={x|-2<x<1},B={x|2x>1},则A∩(∁RB)为( )
| A. | (-2,1) | B. | (-∞,1) | C. | (0,1) | D. | (-2,0] |
13.为了得到函数y=sin(2x-$\frac{π}{5}$),x∈R的图象,只需将函数y=sin2x,x∈R的图象上所有的点( )
| A. | 向左平行移动$\frac{π}{5}$个单位长度 | B. | 向右平行移动$\frac{π}{5}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{10}$个单位长度 | D. | 向右平行移动$\frac{π}{10}$个单位长度 |
12.某工厂生产某种产品,用传送带将产品送至下一工序,质量员每隔10分钟在传送带某一位置取一件产品进行检验,这种抽样的方法为( )
| A. | 分层抽样 | B. | 简单随机抽样 | C. | 系统抽样 | D. | 其它抽样方式 |
9.曲线y=4x+x2在点(-1,-3)处的切线方程是( )
| A. | y=7x+4 | B. | y=7x+2 | C. | y=x-4 | D. | y=2x-1 |
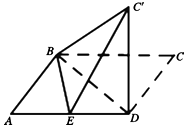 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.