题目内容
已知(
+
)n的展开式中偶数项二项式系数和比(1+x)2n展开式中奇数项二项式系数和小120,求:
(Ⅰ)(1+x)2n展开式中二项式系数最大的项;
(Ⅱ)设(
+
)n展开式中的常数项为p,展开式中所有项系数的和为q,求p+q.
| x |
| 1 | ||
3
|
(Ⅰ)(1+x)2n展开式中二项式系数最大的项;
(Ⅱ)设(
| x |
| 1 | ||
3
|
考点:二项式定理的应用,二项式系数的性质
专题:二项式定理
分析:(Ⅰ)求出n的值,利用二项式的性质即可求(1+x)2n展开式中二项式系数最大的项;
(Ⅱ)根据二项式的通项公式求出p,q即可求p+q.
(Ⅱ)根据二项式的通项公式求出p,q即可求p+q.
解答:
解:由题意得2n-1+120=22n-1,即(2n-16)(2n+15)=0,
∴2n-16=0,解得n=4.
(Ⅰ)(1+x)2n=(1+x)8,则展开式中二项式系数最大的项为第5项;
则T5=
x4=70x4.
(Ⅱ)(
+
)4的通项公式为Tr+1=
(
)4-r•(
)r=
•(
)r•x2-r,
由2-r=0,解得r=0,
则展开式中的常数项T3=
•(
)2=
,
则常数项p=
,
令x=1,则展开式中所有项系数的和q=(1+
)4=
,
则p+q=
+
=
.
∴2n-16=0,解得n=4.
(Ⅰ)(1+x)2n=(1+x)8,则展开式中二项式系数最大的项为第5项;
则T5=
| C | 4 8 |
(Ⅱ)(
| x |
| 1 | ||
3
|
| C | r 4 |
| x |
| 1 | ||
3
|
| C | r 4 |
| 1 |
| 3 |
由2-r=0,解得r=0,
则展开式中的常数项T3=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
则常数项p=
| 2 |
| 3 |
令x=1,则展开式中所有项系数的和q=(1+
| 1 |
| 3 |
| 256 |
| 81 |
则p+q=
| 256 |
| 81 |
| 2 |
| 3 |
| 310 |
| 81 |
点评:本题主要考查二项式展开定理的应用,根据条件求出n的值以及求出二项展开式的通项公式是解决本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
函数f(x)=x3+2x2+mx+1在区间(-∞,+∞)内单调递增,那么m的范围为( )
A、m>
| ||
B、m<
| ||
C、m≥
| ||
D、m≤
|
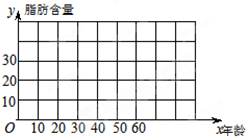 在关于人体脂肪含量y(百分比)和年龄x关系的研究中,得到如下一组数据
在关于人体脂肪含量y(百分比)和年龄x关系的研究中,得到如下一组数据
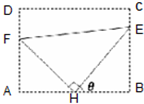 如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10
如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10