Question

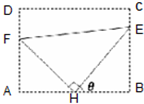如图：某污水处理厂要在一个矩形污水处理池（ABCD）的池底水平铺设污水净化管道（Rt△FHE，H是直角顶点）来处理污水，管道越长，污水净化效果越好．设计要求管道的接口H是AB的中点，EF分别落在线段BC，AD上．已知AB=20米，AD=10

3

米，记∠BHE=θ．
（1）试将污水净化管道的长度L表示为θ的函数，并写出定义域；
（2）若sinθ+cosθ=

2

，求此时管道的长度L；
（3）已知：sinθ+cosθ=

2

sin（θ+

π

4

）（公式）
问：当θ取何值时，污水净化效果最好？并求出此时管道的长度．
（参考值：sin

π

12

=

6 - 2

4

；sin

5π

12

=

6 + 2

4

）

Answer 1

考点：解三角形的实际应用,函数解析式的求解及常用方法

专题：应用题,解三角形

分析：（1）由∠BHE=θ，H是AB的中点，易得EH=

10

cosθ

，FH=

10

sinθ

，EF=

10

sinθ•cosθ

，由污水净化管道的长度L=EH+FH+EF，则易将污水净化管道的长度L表示为θ的函数．
（2）若sinθ+cosθ=

2

，结合（1）中所得的函数解析式，代入易得管道的长度L的值．
（3）污水净化效果最好，即为管道的长度最长，由（1）中所得的函数解析式，结合三角函数的性质，易得结论．

解答： 解：（1）由∠BHE=θ，H是AB的中点，EH=

10

cosθ

，FH=

10

sinθ

，EF=

10

sinθ•cosθ

；
由于BE=10tanθ≤10

3

，且AF=10cotθ≤10

3

，故　θ∈[

π

6

，

π

3

]．
于是L=

10

sinθ

+

10

cosθ

+

10

sinθ•cosθ

．定义域：[

π

6

，

π

3

]-----------（4分）
（2）L=

10

sinθ

+

10

cosθ

+

10

sinθ•cosθ

=

10(sinθ+cosθ+1)

sinθ•cosθ

由　sinθ+cosθ=

2

⇒（sinθ+cosθ）²=2
故　sinθ•cosθ=

1

2

所以　L=20(1+

2

)．----------------（6分）
（3）由L=

10(sinθ+cosθ+1)

sinθ•cosθ

．θ∈[

π

6

，

π

3

]
令sinθ+cosθ=t，则　sinθ•cosθ=

t2-1

2

．-------------（8分）
由sinθ+cosθ=

2

sin(θ+

π

4

)且θ∈[

π

6

，

π

3

]，
有t∈[

2

sin

5π

12

，

2

]即t∈[

1+ 3

2

，

2

]------------（10分）
又L=

20

t-1

在[

1+ 3

2

，

2

]上单调递减于是 当 t=

1+ 3

2

时，L最大为20(

3

+1)．
此时，θ=

π

6

或θ=

π

3

答：当θ=

π

6

或θ=

π

3

时，污水净化效果最好．此时管道的长度为20(

3

+1)米．----------------（12分）

点评：本题考查的知识点是在实际问题中建立三角函数模型及解三角形，根据已知条件构造出L关于θ的函数，是解答本题的关键．