题目内容
函数f（x）=x3+2x2+mx+1在区间（-∞，+∞）内单调递增，那么m的范围为（ ）
A、m＞
| ||
B、m＜
| ||
C、m≥
| ||
D、m≤
|
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：f（x）为三次多项式函数，解决单调性用导数，函数f（x）=x3+2x2+mx+1是R上的单调递增函数即f′（x）≥0在R上恒成立．
解答：
解：f′（x）=3x2+4x+m．
∵f（x）在R上是单调递增函数，
∴f′（x）≥0在R上恒成立，
即3x2+4x+m≥0．
由△=16-4×3m≤0，得m≥
．
故选：C．
∵f（x）在R上是单调递增函数，
∴f′（x）≥0在R上恒成立，
即3x2+4x+m≥0．
由△=16-4×3m≤0，得m≥
| 4 |
| 3 |
故选：C．
点评：本题考查函数单调性的应用：已知单调性求参数范围．一般转化为导函数f′（x）≥0或f′（x）≤恒成立处理．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
为了得到函数y=cos（x+
）的图象，只需要把函数y=cos（x-
）的图象上的所有点（ ）
| π |
| 4 |
| π |
| 4 |
A、向右平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向左平行移动
|
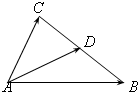
如图，已知△ABC中，D为BC边上的中点，则下列等式中正确的是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
△ABC中，a，b，c分别是角A，B，C所对的边，若A=75°，B=45°，c=2
，则b等于（ ）
| 3 |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
已知O为极点，曲线C1，C2都在极轴的上方，极坐标方程为C1：ρ=2cosθ（0≤θ≤π），C2：ρ=2（0≤θ≤π）．若直线θ=α（ρ∈R，0≤α＜π）与曲线C1，C2交于M，N（M不同于点O）两点，则OM2+MN2的最小值为（ ）
| A、1 | B、2 | C、3 | D、4 |
已知x，y＞0，则
+
+2
的最小值是（ ）
| 1 |
| x |
| 1 |
| y |
| xy |
| A、2 | ||
B、2
| ||
| C、4 | ||
| D、5 |
设f（x）是一次函数，f（8）=15，f（2），f（5），f（14）成等比数列，令Sn=f（1）+f（2）+f（3）+…+f（n），则Sn等于（ ）
| A、n2 |
| B、n2-n |
| C、n2+n |
| D、以上都不对 |