题目内容
已知二次函数f(x)=ax2+bx(a≠0),f(2)=0且方程f(x)=x有两个相等的实数根.
(1)求f(x)的解析式;
(2)求f(x)的最大值.
(1)求f(x)的解析式;
(2)求f(x)的最大值.
考点:二次函数的性质,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)由f(2)=0,且f(x)=x有两个相等的实数根,求出a、b的值,从而得f(x)的解析式;(2)通过配方法求出函数的最大值.
解答:
解:(1)∵f(2)=0,∴4a+2b=0①;
又方程f(x)=x有两个相等的实数根,
即ax2+(b-1)x=0有两个相等的实数根,
∴(b-1)2=0②;
由①②可得,a=-
,b=1,
∴f(x)=-
x2+x;
(2)∵f(x)=-
x2+x
=-
(x-1)2+
∴当x=1时,f(x)有最大值
.
又方程f(x)=x有两个相等的实数根,
即ax2+(b-1)x=0有两个相等的实数根,
∴(b-1)2=0②;
由①②可得,a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
(2)∵f(x)=-
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=1时,f(x)有最大值
| 1 |
| 2 |
点评:本题考查了求函数的解析式以及利用函数的图象与性质求最值,从而得值域的问题,是基础题.

练习册系列答案
相关题目
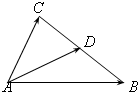
如图,已知△ABC中,D为BC边上的中点,则下列等式中正确的是( )

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
设f(x)是一次函数,f(8)=15,f(2),f(5),f(14)成等比数列,令Sn=f(1)+f(2)+f(3)+…+f(n),则Sn等于( )
| A、n2 |
| B、n2-n |
| C、n2+n |
| D、以上都不对 |