题目内容
已知复数z满足z=
-4．
（1）求复数z的共轭复数
；
（2）若w=z+ai，且|w|≤|z|，求实数a的取值范围．
| -2+6i |
| 1-i |
（1）求复数z的共轭复数
. |
| z |
（2）若w=z+ai，且|w|≤|z|，求实数a的取值范围．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：（1）利用复数的运算法则、共轭复数的定义即可得出；
（2）利用复数模的计算公式、一元二次不等式的解法即可得出．
（2）利用复数模的计算公式、一元二次不等式的解法即可得出．
解答：
解：（1）z=
-4=-8+2i，
∴
=-8-2i．
（2）w=-8+（2+a）i，
∴|z|=2
，
|w|=
=
，
∵|w|≤|z|，
则68+4a+a2≤68，a2+4a≤0，-4≤a≤0，
所以，实数a的取值范围是：-4≤a≤0．
| (-2+6i)(1+i) |
| 2 |
∴
. |
| z |
（2）w=-8+（2+a）i，
∴|z|=2
| 17 |
|w|=
| 64+(2+a)2 |
| 68+4a+a2 |
∵|w|≤|z|，
则68+4a+a2≤68，a2+4a≤0，-4≤a≤0，
所以，实数a的取值范围是：-4≤a≤0．
点评：本题考查了复数的运算法则、共轭复数的定义、复数模的计算公式、一元二次不等式的解法，考查了计算能力，属于基础题．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
已知x，y＞0，则
+
+2
的最小值是（ ）
| 1 |
| x |
| 1 |
| y |
| xy |
| A、2 | ||
B、2
| ||
| C、4 | ||
| D、5 |
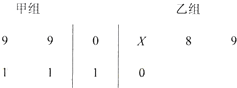以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以X表示．