题目内容
4. 如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
分析 根据山顶的仰角可得AC=1,BP=$\sqrt{2}$BD,过A向乙山作垂线,则AB=2(BD-1),在△ABP中使用余弦定理列方程解出BD.
解答 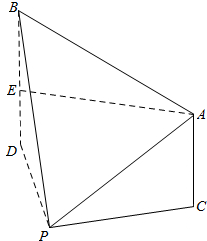 解:假设甲山底部为C,乙山底部为D,过A作AE⊥BD于E.
解:假设甲山底部为C,乙山底部为D,过A作AE⊥BD于E.
由题意可知∠APC=30°,∠BPD=45°,AP=2,
∴AC=AP•sin30°=1,DE=AC=1,设BD=h,则DP=BD=h,BE=h-1,∴BP=$\sqrt{2}$h.
∵∠BAE=30°,∴AB=2BE=2h-2.
在△ABP中,由余弦定理得:cos45°=$\frac{A{P}^{2}+B{P}^{2}-A{B}^{2}}{2AP•BP}$=$\frac{4+2{h}^{2}-({2h-2)}^{2}}{4\sqrt{2}h}$=$\frac{\sqrt{2}}{2}$.
解得h=2.
∴乙山的高度为2km.
故答案为:2.
点评 本题考查了余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
14.执行如图所示的程序框图,输出的S值是( )
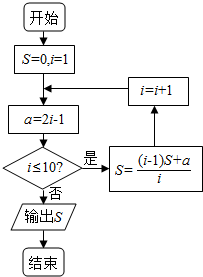

| A. | 10 | B. | 20 | C. | 100 | D. | 120 |
14.$\root{3}{(lg5-1)^{3}}$-$\sqrt{(lg2-1)^{2}}$=( )
| A. | lg$\frac{2}{5}$ | B. | 1 | C. | -1 | D. | lg$\frac{5}{2}$ |