题目内容
9.已知a=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$,b=$\underset{lim}{△x→0}$$\frac{f({x}_{0}-△x)-f({x}_{0})}{△x}$,
c=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+2△x)-f({x}_{0})}{△x}$,
d=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0}-△x)}{2△x}$,
e=$\underset{lim}{x→{x}_{0}}$$\frac{f(x)-f({x}_{0})}{x-{x}_{0}}$,
则b,c,d,e中与a相等的是( )
| A. | c,d | B. | d,e | C. | b,e | D. | c,e |
分析 由题意和极限的定义可得a=f′(x0),由极限的定义分别计算b、c、d、e可得.
解答 解:∵a=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$=f′(x0),
∴b=$\underset{lim}{△x→0}$$\frac{f({x}_{0}-△x)-f({x}_{0})}{△x}$=-$\underset{lim}{-△x→0}$$\frac{f[{x}_{0}+(-△x)]-f({x}_{0})}{-△x}$=-f′(x0)=-a,
∴c=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+2△x)-f({x}_{0})}{△x}$=2•$\underset{lim}{2△x→0}$$\frac{f({x}_{0}+2△x)-f({x}_{0})}{2△x}$=2f′(x0)=2a,
∴d=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0}-△x)}{2△x}$=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0})+f({x}_{0})-f({x}_{0}-△x)}{2△x}$,
=$\frac{1}{2}$$\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$-$\frac{1}{2}$$\underset{lim}{△x→0}$$\frac{f({x}_{0}-△x)-f({x}_{0})}{△x}$=$\frac{1}{2}$a+$\frac{1}{2}$a=a,
∴e=$\underset{lim}{x→{x}_{0}}$$\frac{f(x)-f({x}_{0})}{x-{x}_{0}}$=$\underset{lim}{△x→0}$$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$=f′(x0)=a
故选:B
点评 本题考查极限的运算,涉及导数的定义和整体思想,属基础题.

| A. | S4 | B. | S5 | C. | S6 | D. | S7 |

| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
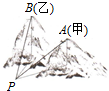 如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.